Алгебраическая форма записи комплексных чисел

Легко видеть, что произведение b·i = (b,0)·(0,1) = (b·0–0·1, b·1+0·0) = (0,b) и c=(a,b)=(a,0)+(0,b). Поэтому c=a+b·i – алгебраическая форма записи комплексного числа.

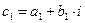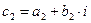Пользуясь алгебраической формой записи комплексного числа, легко показывается, что произведение комплексных чисел и можно вычислить по правилу умножения многочлена на многочлен с заменой i² на -1.

с₁·с₂ = (а₁+b₁·i)·(а₂+b₂·i)=а₁·а₂+а₁·b₂·i+а₂·b₁·i +b₁·b₂·i² =

= (а₁·а₂-b₁·b₂)+i(а₁·b₂+а₂·b₁) = (а₁·а₂-b₁·b₂,а₁·b₂+а₂·b₁)

Комплексные числа 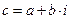и 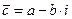называются сопряженными числами.

Легко доказывается, что операция сопряжения обладает свойствами:

1.

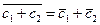
2.

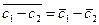
3.

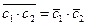
4.

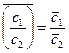
Произведение 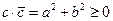, неравенство будет строгим, если с ≠ 0. Во множестве комплексных чисел существует единственное число 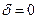, такое что 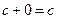, и в множестве комплексных чисел существует единственное числ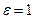о , что .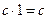

Пусть с₁ = а₁+b₁·i и с₂ = а₂+b₂·i , причем с₂ ≠ 0, тогда частное 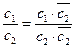, таким образом будет найдено частное.