Арифметические действия над комплексными числами
Под суммой двух комплексных чисел 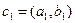 и
и 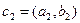 понимается комплексное число с = (а1+ а2, b1+b2) и обозначается с = с1+с2 .
понимается комплексное число с = (а1+ а2, b1+b2) и обозначается с = с1+с2 .
Вычитание определяется как действие обратное сложению.
Под разностью двух комплексных чисел 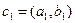 и
и 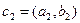 понимается комплексное число с, такое что с1 = с+с2 и обозначается с = с1-с2. Оказывается, что эта разность единственная и притом равна
понимается комплексное число с, такое что с1 = с+с2 и обозначается с = с1-с2. Оказывается, что эта разность единственная и притом равна 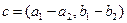 .
.
Произведением двух комплексных чисел 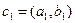 и
и 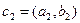 называется комплексное число с равное
называется комплексное число с равное 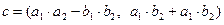 . Действие деления определяется как обратное умножению.
. Действие деления определяется как обратное умножению.
Под частным двух комплексных чисел 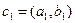 и
и 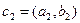 понимается комплексное число
понимается комплексное число 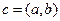 , такое что с1 = с·с2 . Частное обозначается символом с = с1/c2 . Оказывается, что частное существует и единственно, если с2 ≠ 0 (c1/0 = c; c1 = 0·с = 0; 0/0 = c; 0 = 0·с).
, такое что с1 = с·с2 . Частное обозначается символом с = с1/c2 . Оказывается, что частное существует и единственно, если с2 ≠ 0 (c1/0 = c; c1 = 0·с = 0; 0/0 = c; 0 = 0·с).
Действия сложения и умножения комплексных чисел обладают обычными арифметическими свойствами:
· с1 + (с2 + с3) = (с1 +с2) + с3 (ассоциативность сложения)
· с1 · (с2 · с3) = (с1 · с2) · с3 (ассоциативность умножения)
· с1 + с2 = с2 + с1 (коммутативность сложения)
· с1 · с2 = с2 · с1 (коммутативность умножения)
· с1 · (с2 + с3) = с1 · с2 + с1 · с3 (дистрибутивность умножения относительно операции сложения)
Среди комплексных чисел выделяют число (0,1), которое обозначается символом i. Это число обладает характеристическим свойством:
i2 = i·i = -1
Действительно i·i = (0,1)·(0,1) = (0·0-1·1, 0·1+1·0) = (-1,0) = -1
Часто пишут неправильно, что 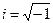 . На самом деле -
. На самом деле - 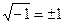 .
.
Дата добавления: 2015-06-12; просмотров: 1342;
