Пример. Выразить cos3α и sin 3α через cosα и sinα.

Выразить cos3α и sin 3α через cosα и sinα.

В силу формулы Муавра имеем: (cos3α+ i·sin3α) = (cosα+ i·sinα)³ =

cos³α + i·3·cos²α·sinα - 3·cosα·sin²α - i·sin³α

cos3α = cos³α - 3·cosα·sin²α

sin3α = 3·cos²α·sinα - sin³α

Найти (1+i)²⁰

c = 1+i·|c|=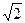

Arg c =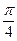

1 + i = 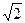· ( cos 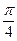+ i·sin )

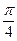(1+i)²⁰ = 2¹⁰· (cos 5π +i·sin 5 π) = -2¹⁰ = -1024

Рассмотрим два комплексных числа с₁ и с₂, с₂ ≠ 0. 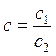. По определению частного с₁ = с·с₂ = 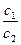·с₂.

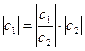
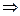
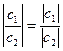
Arg c₁ = Arg 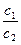+ Arg c₂

Arg 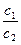= Arg c₁ - Arg c₂

Итак, с = 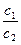= 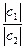[cos(Arg c₁ - Arg c₂)+i·sin(Arg c₁ - Arg c₂)]

Комплексное число с = 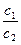изображается вектором, который получается из вектора с₁ путем его сжатия в 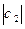раз, затем поворотом полученного вектора на угол (-Arg c₂)

Корень n – ой степени из комплексного числа

Возьмем произвольное комплексное число с и натуральное число n 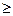2.

Комплексное число Z называется корнем n–ой степени из комплексного числа c, если Zⁿ = c.

Найдем все значения корня n–ой степени из комплексного числа с. Пусть c=|c|·(cos Arg c+i·sin Arg с), а Z = |Z|·(сos Arg Z + i·sin Arg Z), где Z корень n-ой степени из комплексного числа с. Тогда должно быть 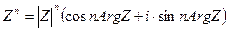= c = |c|·(cos Arg c+i·sin Arg с). Отсюда следует, что 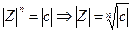и n·Arg Z = Arg с 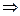Arg Z = 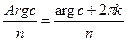(k=0, 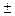1,…). Следовательно, Z = 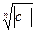(cos 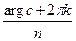+ i·sin 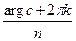), (k=0, 1,…). Легко увидеть, что любое из значений 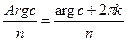, (k=0, 1,…) отличается от одного из соответствующих значений 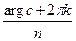,(k = 0,1,…,n-1) на кратное 2π. Поэтому 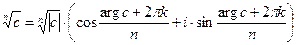, (k = 0,1,…,n-1).