Пример. Рассмотрим функцию W = = x-i·y
Рассмотрим функцию W = 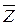 = x-i·y. Покажем, что эта функция не имеет производной ни в одной точке. Возьмем любую точку Z0 = x0+i·y0, придадим ей приращение ΔZ = Δx+i·Δy, тогда функция получит приращение
= x-i·y. Покажем, что эта функция не имеет производной ни в одной точке. Возьмем любую точку Z0 = x0+i·y0, придадим ей приращение ΔZ = Δx+i·Δy, тогда функция получит приращение 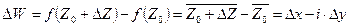 . Значит
. Значит 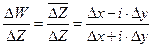

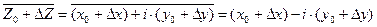 ,
, 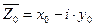 ,
, 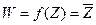
Будем вначале рассматривать ΔZ = Δx + i·Δy такие, что Δx → 0, а Δy = 0, т. е. точка Z0 + ΔZ → Z0 по горизонтальной прямой. При этом мы получим, что 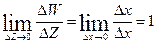
Будем теперь рассматривать приращение ∆Z такими, что ∆x = 0, а ∆y → 0, т.е. когда Z0 + ∆Z→ Z0 по вертикальной прямой, при этом очевидно будет 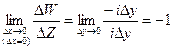 .
.
Полученные пределы различные, поэтому отношение 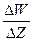 не имеет предела при ∆Z → 0, то есть функция
не имеет предела при ∆Z → 0, то есть функция 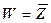 не имеет производной в любой точке Z0 .
не имеет производной в любой точке Z0 .
Выясним смысл производной по множеству. Пусть E – действительная ось, и W = f(Z) = x, тогда это есть обычная вещественная функция вещественной переменной f(x) = x и ее производная будет равна 1 ( 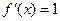 ).
).
Пусть теперь Е – это вся плоскость (Z). Покажем, что функция f(Z) = x в этом случае не имеет производной ни в одной точке. Действительно, в данном случае  . Отсюда видно, что если
. Отсюда видно, что если 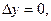 а
а 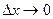 , то
, то 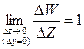 . Если же
. Если же 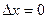 , а
, а 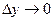 , то
, то 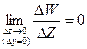 . Следовательно, отношение
. Следовательно, отношение 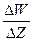 не имеет предела при
не имеет предела при 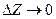 , поэтому функция f(Z) = x не имеет производной ни в одной точке
, поэтому функция f(Z) = x не имеет производной ни в одной точке  .
.
Отметим, что если рассматривается комплексно-значная функция вещественной переменной 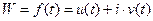 , то из определения производной непосредственно вытекает, что
, то из определения производной непосредственно вытекает, что 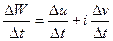 , следовательно,
, следовательно,  (это производная по вещественной оси).
(это производная по вещественной оси).
Дата добавления: 2015-06-12; просмотров: 974;
