Теорема. Для того чтобы функция W = f(Z) была дифференцируема в точке Z0, необходимо и достаточно, чтобы она имела в этой точке конечную производную

Для того чтобы функция W = f(Z) была дифференцируема в точке Z₀, необходимо и достаточно, чтобы она имела в этой точке конечную производную 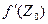, при этом всегда оказывается, что в представлении (2) .

Доказательство.

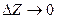Необходимость. Пусть функция дифференцируема в точке Z₀. Покажем, что она имеет в этой точке конечную производную, и что эта производная равна числу А. В силу дифференциации f(Z) в точке Z₀ имеет место представление (2), значит (3). Производя здесь предельный переход при получим, что , значит .

Достаточность. Пусть функция f(Z) имеет в точке Z₀ конечную производную 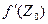. Покажем, что имеет место представление (2). В силу существования производной 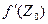имеет место представление (1), но это и есть представление (2), в котором A = 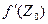. Достаточность установлена.

Как мы знаем, дифференциал 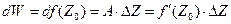, принимая в качестве дифференциала независимой переменной Z ее приращение , то есть, полагая , мы можем записать и поэтому (это отношение дифференциалов, а не единый символ).