Теорема. Пусть в плоскости (Z) даны некоторая прямая или окружность и дробно-линейное отображение
Пусть в плоскости (Z) даны некоторая прямая или окружность  и дробно-линейное отображение
и дробно-линейное отображение
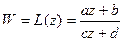 (1) с
(1) с 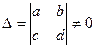 .
.
Пусть Г – это образ линии  при отображении (1),
при отображении (1), 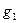 ,
,  и
и 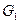 ,
, 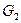 – это соответственно области комплексной плоскости, ограниченные линиями
– это соответственно области комплексной плоскости, ограниченные линиями  и Г, тогда дробно-линейная функция (1) отображает любую из областей
и Г, тогда дробно-линейная функция (1) отображает любую из областей 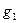 ,
,  на одну из областей
на одну из областей 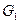 или
или 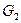 . Причем различные области
. Причем различные области 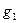 и
и  отображаются на различные области
отображаются на различные области 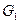 и
и 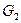 .
.

Доказательство.
Возьмем две произвольные точки 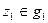 и
и 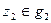 , так как отображение (1) взаимно однозначно и отображает
, так как отображение (1) взаимно однозначно и отображает  на Г, то образы
на Г, то образы  точек
точек 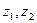 не будут лежать на Г. Покажем, что одна из этих точек
не будут лежать на Г. Покажем, что одна из этих точек  принадлежит области
принадлежит области 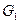 , а вторая –
, а вторая – 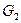 .
.
Пусть для определенности 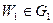 . Мы покажем, что
. Мы покажем, что 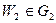 . Предположим противное: пусть точка
. Предположим противное: пусть точка 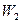 также принадлежит
также принадлежит 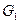 . Тогда эти две точки мы можем соединить отрезком прямой или дугой окружности, не пересекающим линии Г.
. Тогда эти две точки мы можем соединить отрезком прямой или дугой окружности, не пересекающим линии Г.
В силу кругового свойства дробно-линейной функции прообразом этого отрезка в плоскости (Z) является отрезок прямой или окружности, соединяющий точки 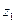 и
и 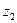 . Причем этот отрезок не пересекается с линией
. Причем этот отрезок не пересекается с линией  . Но такой отрезок не существует, так как
. Но такой отрезок не существует, так как 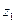 и
и 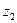 лежат в различных областях, ограниченных линией
лежат в различных областях, ограниченных линией  . Мы получили противоречие, следовательно,
. Мы получили противоречие, следовательно, 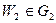 .
.
Зафиксируем теперь точку 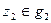 , а
, а 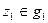 будем считать переменной точкой. Тогда ясно, что все точки
будем считать переменной точкой. Тогда ясно, что все точки 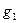 отображаются в точки множества
отображаются в точки множества 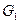 . Аналогично, фиксируя
. Аналогично, фиксируя 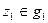 и рассматривая
и рассматривая 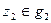 как переменную точку, мы устанавливаем, что область
как переменную точку, мы устанавливаем, что область  отображается в область
отображается в область 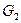 .
.
Нам остается доказать, что 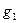 отображается на всю область
отображается на всю область 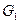 , а
, а  – на всю
– на всю 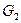 . Возьмем произвольную точку
. Возьмем произвольную точку  , обозначим ее прообраз через
, обозначим ее прообраз через  . Так как
. Так как 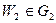 , то прообразы
, то прообразы  и
и 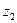 обязательно должны принадлежать различным областям
обязательно должны принадлежать различным областям 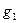 и
и  (так как
(так как 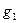 отображается в
отображается в 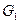 , а
, а  – в
– в 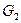 , так как в противном случае
, так как в противном случае 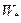 и
и 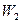 принадлежали бы одной области). Но точка
принадлежали бы одной области). Но точка 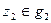 , значит
, значит  , отсюда и следует, что
, отсюда и следует, что 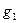 отображается на
отображается на 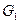 .
.
Аналогичным образом показывается, что  отображается на
отображается на 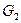 .
.
Дата добавления: 2015-06-12; просмотров: 1022;
