Построение дробно-линейной функции, заданной в трех точках

Найдем вначале дробно-линейную функцию 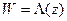, которая в различных точках 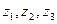принимает соответствующие значения 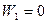, , 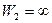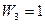. Очевидно 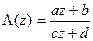– общий вид этой функции. Так как 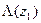равно нулю ( 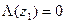), то обязательно 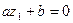. Поэтому .

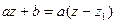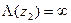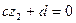Аналогично, так как , то и поэтому 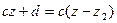, значит .

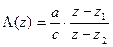Наконец, в силу 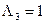получаем 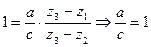: 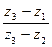. Аналогично получаем : .

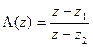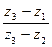Найдем теперь отображение 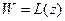, которое переводит три различные конечные точки 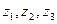соответственно в три различные конечные точки 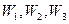: 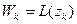. Легко видеть, что отображение 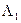, переводящее точки 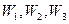соответственно в имеет вид 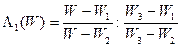. Ясно, что отображение 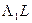будет переводить точки 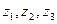в . Поэтому 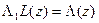, применяя к обеим частям равенства отображение 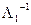, получим .

Обычно для отображения 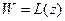пользуются не последней формулой, предыдущей. При этом обозначают 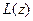через W. В результате получают равенство 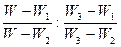= 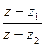: 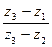(2). Отсюда и находят .

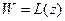Отметим, что если одна из точек 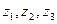или одна из точек 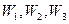обращаются в 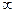, то разности, в которых участвуют эти точки в равенстве (2) замещаются на (1).