Доказательство. Построим дробно-линейную функцию (1)
Построим дробно-линейную функцию (1). Она обладает свойством (2) h(zk)=Wk и отображает линию γ на  Г. Покажем, что эта дробно-линейная функция отображает область g на область G.
Г. Покажем, что эта дробно-линейная функция отображает область g на область G.
Мы знаем, что дробно-линейная функция осуществляет конформные отображения 1го рода. Поэтому, если отрезок δ, являющийся нормалью к линии γ, проведенной через точку z2 внутрь области g, т. е. влево от наблюдателя, стоящего в точке z2 и стоящего вдоль линии γ в выбранном направлении, то его образ Δ определен (также являющимся отрезком прямой или другой окружности) будет также направлен в левую сторону от наблюдателя, стоящего в точке W2 и стоящего вдоль линии Г ввыбранном направлении. Следовательно, этот образ 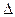
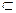 G, следовательно, h(g) = G.
G, следовательно, h(g) = G.
Отобразить взаимнооднозначно и конформно верхнюю полуплоскость 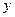 > 0 на внутренности единичной окружности.
> 0 на внутренности единичной окружности.

Пусть z1 = -1, z2 = 0, z3 = 1, W1 = 1, W2 = i, W3 = -1.
Тогда, по предыдущей теореме дробно-линейная функция, определяемая уравнением 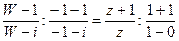 , будет отображать верхнюю полуплоскость g на внутренность G единичного круга. Можно показать, что эта функции равна
, будет отображать верхнюю полуплоскость g на внутренность G единичного круга. Можно показать, что эта функции равна 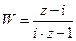 .
.
Дата добавления: 2015-06-12; просмотров: 920;
