Пример. Инвариантность двойного отношения при дробно-линейном преобразовании.

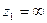, тогда вместо , .

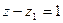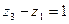Инвариантность двойного отношения при дробно-линейном преобразовании.

Рассмотрим четыре различные точки a, b, c, d, тогда двойное отношение называется двойным или ангарническим отношением.

В случае, когда одно из этих чисел a, b, c, d обращается в 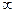, разности отношения, в котором участвует эта 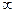заменяется на 1. Двойное отношение обозначают символом (a, b, c, d).

Рассмотрим четыре произвольных числа a, b, c, d и какое-нибудь дробно-линейное отображение 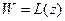, переводящее их соответственно в числа A, B, C, D. Так как a, b, d L переводит в A, B, D, то оно имеет вид:

.

Так как W = h(z) переводит c в C, то будет выполняться равенство:

,

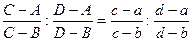т. е. (A,B,C,D)=(a,b,c,d).

Итак, всякая дробно-линейная функция составляет инвариантное двойное отношение комплексных чисел.