Показательная функция

W = e^Z (1)

Показательная функция W = e^Z определяется формулой e^Z = e^x(cosy+i∙siny) (2), где Z = x+i∙y. Вместо e^Z пользуются обозначением exp Z (экспонент Z).

Свойства показательной функции:

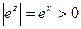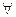1. Из формулы (2) непосредственно следует, что для Z (Z - конечно), ( 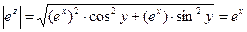). Arge^x = y+2kπ, k 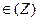. Отсюда следует, что функция W = e^Z не обращается в нуль ни в одной точке.

2. Очевидно, если Z = i∙y (x = 0), то e^i∙y = cosy+i∙siny. Это равенство позволяет записывать комплексные числа в тригонометрической форме. Действительно, если Z = Z(cosφ+i∙sinφ), где Z = |Z|, φ = argZ, то очевидно будет Z = Z·e^i∙φ (3). Это и есть показательная форма записи комплексного числа.

3. Очевидно Z = x (т. е. y = 0), то e^Z = e^x, т.е. эта функция совпадает с вещественной показательной функции.

4. Справедливо равенство [e^Z]' = e^Z (для 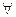Z).