Доказательство. Очевидно у функции W = eZ вещественная часть u=ex·cosy, а мнимая часть v=ex·siny
Очевидно у функции W = eZ вещественная часть u=ex·cosy, а мнимая часть v=ex·siny. Эта функция имеет конечно непрерывные частные производные первого порядка и следовательно являются дифференцируемыми в любой точке. Причем справедливы равенства:
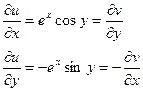
Следовательно, по известной теореме о существовании производной комплексной функции в точке функции W = eZ имеет конечную производную в любой точке Z, и эта производная будет равна:
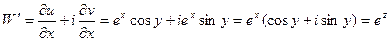
Теорема сложения.
Для любых двух комплексных чисел Z1 = x1+i∙y1 и Z2=x2+i∙y2 справедливо равенство 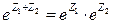 .
.
Дата добавления: 2015-06-12; просмотров: 854;
