Доказательство. Пусть функция f(x) интегрируема на [a, b], тогда

Пусть функция f(x) интегрируема на [a, b], тогда 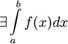. По определению интеграла 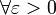, то есть для 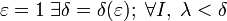и любого набора точек 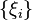выполняется:

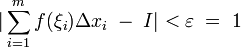, отсюда получаем:

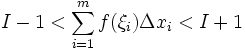
Допустим, что функция не ограничена на [a, b], то есть не ограничена на некотором 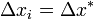. Обозначим остальную, не относящуюся к данному отрезку часть суммы за σ:

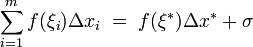
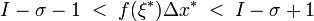
В силу неограниченности всегда можно выбрать такое ξ*, что .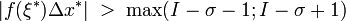

Получено противоречие, следовательно интегрируемая функция должна быть ограниченной.