Основные свойства определенного интеграла.

Основные свойства определённого интеграла.

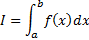
1) ;

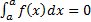2) 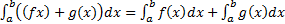; (следует из определения интеграла как предела интегральных сумм).

3) ;

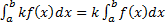4) ;

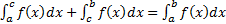5) ;

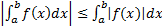6) ;

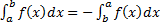Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и
.
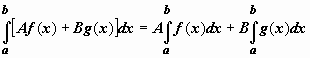Док-во: для любого разбиения отрезка и любого выбора точек 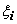выполняется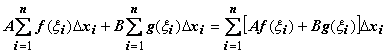

Перейдем в этом равенстве к пределу при 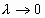. Так как существуют пределы интегральных сумм, стоящих в левой части равенства, то существует предел линейной комбинации этих сумм, следовательно, существует предел правой интегральной суммы, откуда следует истинность и утверждения, и равенства.

Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то .
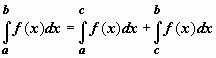Док-во. Если f(x) удовлетворяет условиям интегрируемости по отрезку [a,b], то она удовлетворяет условиям интегрируемости по отрезкам [a,c] и [c,b]. Будем брать такие разбиения отрезка [a,b] , чтобы точка c являлась одним из узлов x_i: c = x_i0, . Тогда .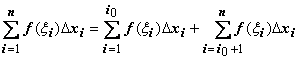

В этом равенстве первая сумма справа - интегральная сумма для 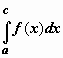, вторая - для 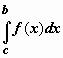. Переходим к пределу при 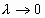. Пределы для всех трёх сумм существуют, и .

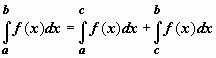Свойство аддитивности остаётся верным при любом расположении точек, если только функция интегрируема по самому широкому интервалу. Пусть, например, c < b < a, и f(x) интегрируема по [c, a]. Тогда, по доказанному, 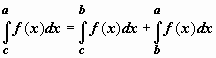. Отсюда и из определения интеграла для случая, когда нижний предел больше верхнего, следует, что .

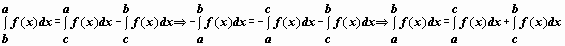Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то

.
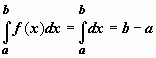Док-во. Если f(x) = 1 , то для любого разбиения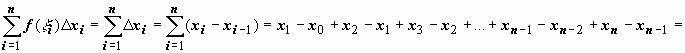
= xn - x0 = b – a, т.е любая интегральная сумма равна длине отрезка. Предел постоянной равен этой постоянной, откуда и следует доказываемое утверждение.

Теорема об интегрировании неравенств. Если в любой точке 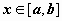выполняется неравенство 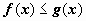, и функции f(x), g(x) интегрируемы по отрезку [a,b], то .
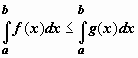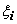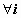
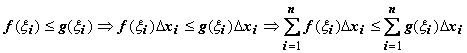Док-во. Для любого разбиения отрезка и любого выбора точек при . Переходя в этом неравенстве к пределу при 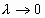, получаем требуемое неравенство.

Теоремы об оценке интеграла.
1. Если на отрезке [a,b] функция удовлетворяет неравенству 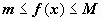, то .
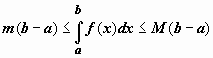Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств): .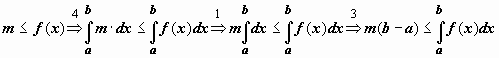

Аналогично доказывается и правое неравенство.
2. Если функция f(x) интегрируема по отрезку [a,b], то .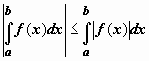
Док-во.

.
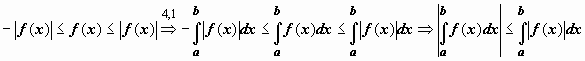Теорема о среднем. Если f(x) непрерывна на отрезке [a,b], то существует точка 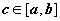, такая что .
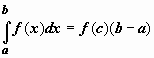Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда 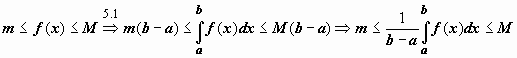. Число 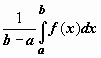заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка 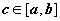, такая что .
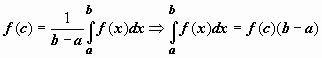Это свойство имеет простую геометрическую интерпретацию: если 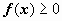непрерывна на отрезке [a,b], то существует точка 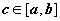такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).