Формула Ньютона-Лейбница для определенного интеграла.

Теорема:

Условие: f(t) непрерывна на [a, b], а F(x) ее любая первообразная.

Утверждение: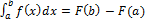

Доказательство: Рассмотрим некоторую первообразную F (x) функции f (x). По Следствию из Теоремы «О дифференцируемости интеграла с переменным верхним пределом» (см. предыдущий вопрос) она имеет вид 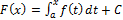. Отсюда

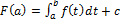=> c=F(a), и

.

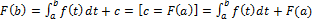Перенесем F(a) в последнем равенстве в левую часть, переобозначим переменную интегрирования снова через x и получим формулу Ньютона – Лейбница:

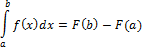
Замечание 3.1. Доказанное равенство

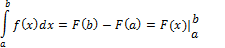
называется формулой Ньютона – Лейбница.