Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
Вычисление площадей плоских фигур:
Прямоугольные координаты
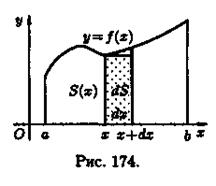Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:
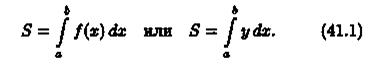
Формула (41.1) получена путем применения метода сумм. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см. рис. 174).
Для нахождения площади S этой трапеции проделаем следующие операции:
1. Возьмем произвольное х [а; b] и будем считать, что S = S(x).
2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у • dx.
3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем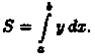 
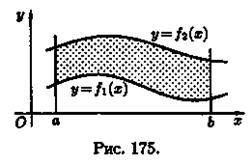Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле
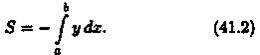
Формулы (41.1)и (41.2) можно объединить в одну:
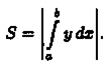
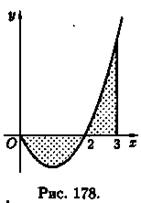
Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадь находится по формуле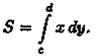 
И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически
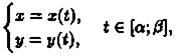
прямыми х = а и х = b и осью Ох, то площадь ее находится по формуле
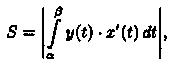
где а и β определяются из равенств х(а) = а и х(β) =b.
Полярные координаты
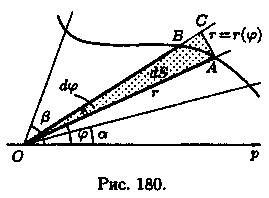
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180).
1. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).
2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.
Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она заштрихована) радиуса r с центральным углом dφ. Поэтому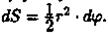 
3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь
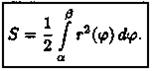
Вычисление длины дуги плоской кривой
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
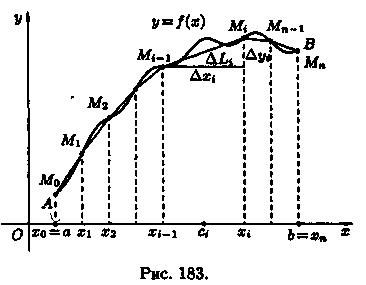
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у' = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
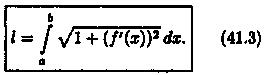
1. Точками х0 = а, х1..., хn = b (х0 < x1 < ...< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пусть этим точкам соответствуют точки М0 = А, M1,...,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,..., Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,..., ΔLn. Получим ломаную M0M1M2 ... Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+...+ ΔLn =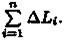 
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
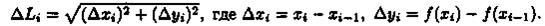
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
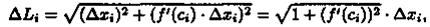
а длина всей ломаной M0M1... Мn равна
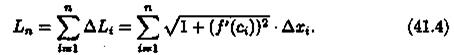
3.Длина l кривой АВ, по определению, равна
.
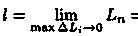
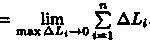Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =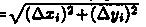 
и, следовательно, |Δxi|<ΔLi).
Функция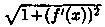 
непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
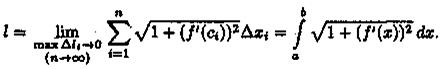
Таким образом,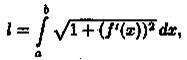 
или в сокращенной записи l =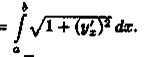 
Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.
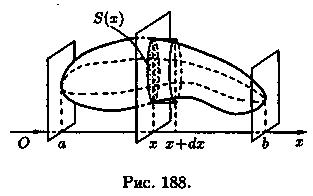1. Через произвольную точку х є [a;b] проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x) (v(a) = 0, v(b) = V).
2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.
3. Находим искомую величину V путем интегрирования dA в пределах от а до В:
Полученная формула называется формулой объема тела по площади параллельных сечений.
Объем тела вращения
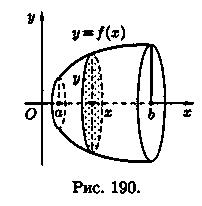
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=πy2.
Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем
Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,
у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен
Дата добавления: 2015-05-16; просмотров: 4299;