Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.

Выражение 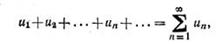(1)

где (uk)kÎN — заданная числовая последовательность, называется числовым рядом. Конечные суммы S1 = u1, S2 = u1 + u2, .... Sn = u1 + u2 +...+ un, называются частичными суммами ряда (1).

Если существует конечный предел последовательности частичных сумм (2)

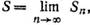то ряд (1) называется сходящимся, а число S—суммой ряда (1)

Необходимое условие сходимости:

Если ряд (1) сходится, то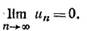

Доказательство:

Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел 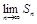=S. Тогда имеет место также равенство 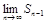=S, так как при n 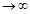и (n-1) 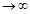. Вычитая почленно из первого равенства второе, получаем 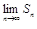- 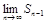= = 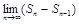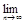un=0, что и требовалось доказать.

Критерий Коши:

Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого ε > 0 су­ществовало N = N(ε) такое, что для всех n > N и р = 1, 2, … выполнялось неравенство:

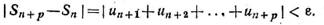
Доказательство:

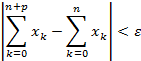
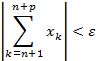
Частный случай:

При 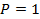: 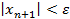, следовательно, 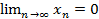(необходимое условие сходимости ряда).