Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.

Следствие №3 (из критерия Коши) :

Если f(x) ограничена и монотонна на [a, b], то она интегрируема на этом отрезке.

Доказательство:

;

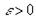
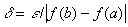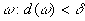
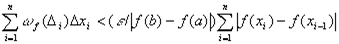
в силу монотонности функции все разности под знаком модуля в получившейся сумме имеют один знак

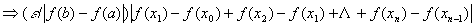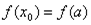{т.к. и 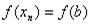}= 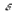ч.т.д.

Следствие №2 (из критерия Коши) :

Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Доказательство:

f - непрерывна на [a, b] 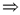она равномерно непрерывна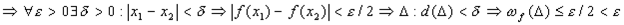

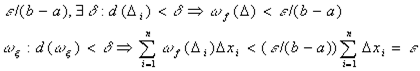ч.т.д.