Доказательство.
Чтобы доказать справедливость этих формул, сначала этого выделим формулу Эйлера. Для этого умножим обе части второй формулы равенства(2) на i: 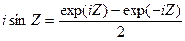 .
.
Складываем первую формулу с полученной:
cosZ+i∙sinZ=exp(iZ) (формула Эйлера), Z заменим на Z1+Z2.
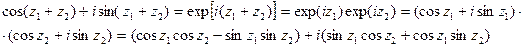 (4)
(4)
Вместо Z1 и Z2 мы поставим (-Z1) и (-Z2).
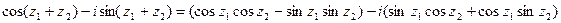 (5)
(5)
Складывая и вычитая (4) и (5), получим
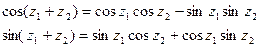 (6)
(6)
Пусть теперь Z1 = Z и Z2 = -Z, подставим и получим
1 = cos2Z+sin2Z
(cos(Z-Z)=cosZ∙cosZ+sinZ∙sinZ).
С тригонометрическими функциями cosZ и sinZ тесно связаны гиперболические функции: chZ - гиперболический косинус Z и shZ - гиперболический синус Z.
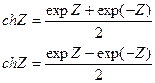 (7)
(7)
chZ = cos(iZ); shZ = -i∙sin(iZ)
Определим действительные и мнимые части функций cosZ и sinZ.
Пусть Z = x+i∙y
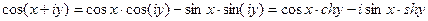
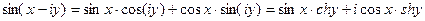
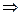 действительная часть
действительная часть
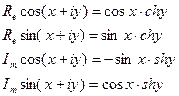
Она ввела функции cosZ и sinZ, используя формулы:
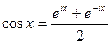 ;
; 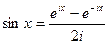
Поясним откуда взялись эти формулы:
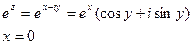
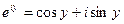 (1)
(1)
y заменим на –y
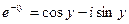 (2)
(2)
Сложим и разделим на два: 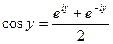 , если из (1) вычели (2) и разделим на 2i, то получим:
, если из (1) вычели (2) и разделим на 2i, то получим: 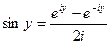 (ну а y можно заменить на x).
(ну а y можно заменить на x).
Вывели равенства:
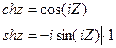
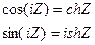 (*)
(*)
Т. к. 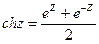
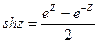
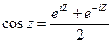
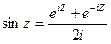
Подставим вместо Z точку iZ :
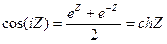
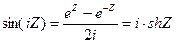
(умножим числитель и знаменатель на i).
ch2Z - sh2Z = 1 (возведем (*) в квадрат).
Отделим действительную и мнимую части:
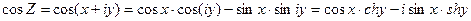
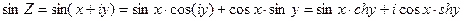
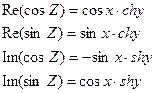
Найдем модули функций cosZ и sinZ. Очевидно,
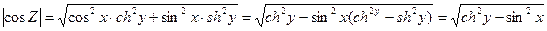
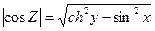 (8)
(8)
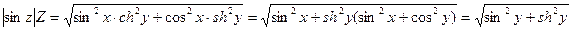 (9)
(9)
Из формул (8) и (9) непосредственно вытекает, что:
(заменим в (8) sin2x на 1, отбросим в (9) sin2x)
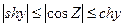 (10)
(10)
(отбросим в (8) sin2x, заменим в (9) sin2x на 1)
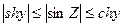 (11)
(11)
( 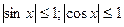
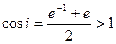 )
)
Дата добавления: 2015-06-12; просмотров: 4036;
