Тригонометрические функции cosZ, sinZ

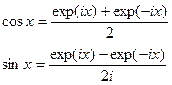формулы Эйлера.

Правые части этих формул определены для 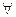комплексного и является аналитическими функциями, поэтому естественно cosZ определяется по формуле:

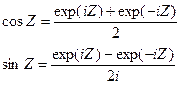(2)

Рассмотрим свойства тригонометрических функций:

1. cosZ - четная функция,

sinZ - нечетная функция

Действительно,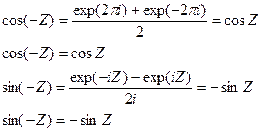

2. Косинус Z и синус Z (cosZ, sinZ),периодические функции с периодом 2π 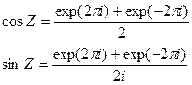, т. е. при замене Z на 2π аргументы показательной функции в правых частях изменяются на ±2π ,т.е. есть периоды показательной функции.

Покажем, что 2π есть основной период функции cosZ и sinZ. Пусть w есть период cosZ, тогда cos(Z+w)=cosZ (по определению периода) при 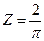получим:

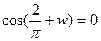,тогда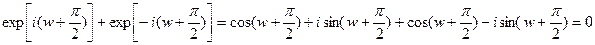

это можно записать: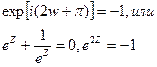

По формуле (1) (Z=i(gw+ 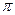)) 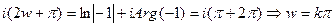, т. к. cosw = cos0 = 1

Следовательно, k принимает четные значения, т.е. период w = 2π, поэтому 2π - основной период.