Гиперболические функции вещественного переменного.

Вещественные гиперболические функции shx и chx определяются функциями: ,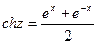

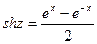
Эти функции заданы на всей числовой оси.

Очевидно, shx нечетна (sh(-x) = -sh(x)), функция chx четная (ch(-x) = chx) (из выше записанных функций).

Следовательно, график функции shx симметричен относительно начала координат, а chx симметричен относительно оси y.

При возрастании x от -∞ до +∞ функция shx возрастает от -∞ до +∞, обращаясь в нуле в 0.

sh0 = 0

Функция chx при возрастании х от -∞ до +∞ убывает от +∞ до 1. При дальнейшем же возрастании х от 0 до +∞, функция chx возрастает от 1 до

+∞.

Из формул для shx и chx непосредственно следует, что разность

chx - shx = e^-x > 0

сh²x - sin²x = 1.

Следовательно, графики этих функций имеют вид, указанный на чертеже.

Из функции (10) и (11) следует, что модули функции |cosZ| и |sinZ| стремятся в бесконечность, когда |y| → ∞.

Из тех же функций следует, что cosZ и sinZ смогут обратиться в нуль лишь на действительной оси, т. е. когда y = 0. По вещественной оси cosZ=cosx; sinZ=sinx. Следовательно, функции cosZ и sinZ обращаются в нуль соответственно только в точках 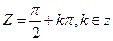(cosZ) и 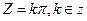(sinZ)

Вычислим производную от cosZ и sinZ. Очевидно:

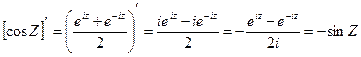
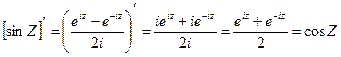
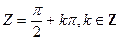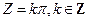Следовательно, функции W = cosZ и W = sinZ являются аналитическими функциями и они осуществляют конформные отображения во всех точках, за исключением соответствующих точек и (т. к. в них производная обращается в нуль).

Пример (конформного отображения c плоскостью показательной функции).

Отобразить конформную полосу ограниченную прямыми y = 0 и y = на верхнюю полость.

Произведем отображение W₁ = e^Z. Оно приведет прямую y = 0 в луч 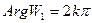(1), а прямую y = в луч (2) .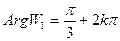

Теперь произведем отображение W = W₁³, это отображение переведет лучи (1) и (2) в лучи , .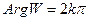

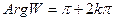Следовательно, функция W = e^3Z и будет искомым отображением.