Пример. которые располагаются в вершинах правильного n-угольника с центром в нуле.

Функция W = 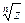(1) (Это то же W = F(Z)). Эта функция является n-значной в 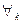точке Z 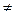0 и ∞ она принимает n значений

(2),

которые располагаются в вершинах правильного n-угольника с центром в нуле.

Очевидно, функция (1) является обратной для аналитической функции

Z=Wⁿ (3).

Функция (3) принимает равные значения во всех точках (2), следовательно, эта функция является n-мерной.

Т. к. функция (3) принимает равные значения в вершинах правильного n-угольника плоскости (W) с центром в нуле (0), то область однолистности не должна содержать ни одной пары таких точек. Наиболее простой областью одномерности функции (3) является внутренность угла раствора 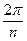с вершиной в нуле.

Следовательно, n-листная плоскость (W) допускает разбиение на n-однолистных областей g_k, являющиеся углами, которые образуют между собой лучи, выходящие из нуля, под углами кратными друг к другу.

Пусть эти лучи составляют с действительной осью и углы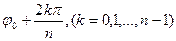

Очевидно, функция (3) отобразит эти лучи в один луч, который составляет с осью x-ов угол: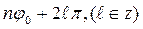

А область g_k отобразится на область 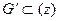, ограниченную этим лучом.

Будем рассматривать функцию (1) на области 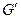ограничивая тем, что ее значение принадлежат некоторой области g_k. Тогда мы получим n однозначных ветвей, которые будем обозначать соответственно.