Логарифмическая функция

Поставим в соответствие 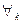Z ≠ 0, множество чисел lnZ получим логарифмическую функцию W = lnZ.

Эта комплексная логарифмическая функция является бесконечной, она определена во всей плоскости (Z), за исключением нуля.

Нетрудно видеть, что эта функция является обратной для показательной функции Z = e^w.

Эта аналитическая функция является однозначной. Она принимает равные значения во всех точках W = lnZ. Следовательно, эта функция является бесконечно-листной.

Т. к. точки, в которых функция Z = e^w принимает равные значения, располагаются на вертикальных прямых на расстоянии кратных 2π друг от друга. То область однолистности этой функции не должна содержать ни одной пары таких точек.

Наиболее простой такой областью однолистности является внутренность горизонтальной полосы ширины 2π.

Т. е. плоскость (W) можно разбить на полосы однолистности, ограниченные горизонтальными прямыми: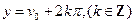

Т. е. эти полосы будут определяться неравенством:

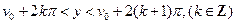(3)

Где 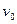- произвольное вещественное число.

Функция Z = e^w отобразит каждую прямую y = 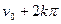в луч, который составит с осью x-ов угол 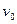, а каждую из рассматриваемых полос на область 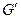, ограниченную этим лучом.

Ограничивая обратную функцию W = lnZ на 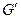тем, что ее значения принадлежат полосе g_k, заданной неравенством (3), мы получим однозначную ветвь W = lnZ.

Очевидно ln_kZ = ln|Z|+i∙Arg_kZ, где Arg_kZ – будет удовлетворять неравенству

(4)