Степень с произвольным показателем

Рассмотрим произвольные комплексные числа a ≠ 0 и α. Под комплексностью степени 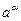будем понимать совокупность e ^lna. Очевидно, если α это рациональное число, то мы получаем

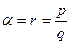
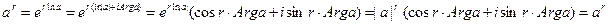
Следовательно, новое определение степени с рациональным показателем совпадает с данным ранее. Легко видеть, что

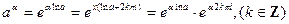
Пусть: 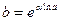, тогда 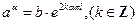(4)

Из формулы (4) вытекает, что если α иррациональное, то 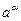имеет бесконечно много значений (при различных k различные значения).

В самом деле, если бы при некоторых значения (4) были бы равны, то было бы 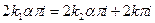, отсюда следовало бы, что 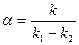- рационально, что невозможно.

Из равенства (4) непосредственно следует, что если α вещественно, то модули всех значений 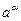равны между собой:

, ( )

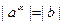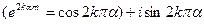Если же α является чисто мнимым числом 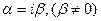, то все числа совокупности 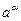будут иметь различные модули (в зависимости от k). В случае когда α имеет вид 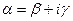, где 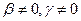, все значения 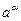будут иметь различные модули, а если β иррационально, то аргументы будут различны (модули различны за счет γ).