Логарифмы

Логарифмом комплексного числа Z ≠ 0, называется множество чисел

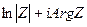(1).

Комплексный логарифм обозначается символом lnZ.

Итак, lnZ=ln|Z|+iArgZ (2).

Как видно, логарифм комплексного числа имеет бесконечное множество значений, все они располагаются на вертикальной прямой, на расстоянии кратных 2π друг от друга.

Как мы знаем, ArgZ = argZ+2kπ, поэтому комплексный логарифм Z равен

ln(Z) = ln|Z|+i·(argZ+2kπ) = (ln|Z|+i∙argZ)+i∙2πk.

Среди значений комплексного логарифма выделяют одно ln|Z|+i·argZ, которое называется главным значением логарифма и обозначается символом

lnZ = ln|Z|+i·argZ

Т. е. lnZ = lnZ+2kπ, (k 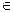Z).

Нетрудно видеть, что множество значений lnZ совпадает с множеством всех решений уравнения e^w=Z, относительно неизвестной W. Т. к. e^w не обращается в 0 ни в одной точке, то число Z = 0 не имеет комплексных логарифмов.

Легко видеть, что если Z = x > 0, то главный логарифм lnZ = lnx (равен вещественному логарифму) (lnx = ln|x|+i·argx = lnx). Все остальные значения комплексного логарифма будут мнимые.

Легко показывается, что для любого комплексного Z, не лежащего на положительной оси x, все значения комплексного логарифма (lnx) мнимые.

Комплексный логарифм обладает свойствами:

1. Для 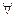Z₁, Z₂ ≠ 0 справедливо равенство: ln(Z₁·Z₂)=lnZ₁+lnZ₂