Понятие поверхности Римара

Рассмотрим функцию: W = 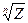. Эта функция является n-значной. Из нее можно выделить n однозначных ветвей. Сделаем это следующем образом. Разобьем плоскость (W) на n равных частей лучами (1) .

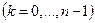Очевидно, функция Z = Wⁿ является однолистной внутри каждого угла.

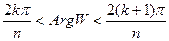(k=0,…,n-1) (2).

Эта функция отображает каждый луч (1) в положительную часть действительной оси, т. е. в луч.

ArgZ = 0+2kπ (3)

Область же (2) отображается на область ограниченную лучом (3). Следовательно, по однозначной функции W = 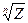определится n однозначных ветвей, которые заданы на одной и той же области, ограниченной лучом (3) и которые принимают значения в области (2).

Эти ветви будут определяться формулами:

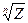( )_k = (k - номер ветви),

где ,(k=0,…,n-1)

Постоим теперь поверхность Римана.

Однозначные ветви (4) мы будем рассматривать на всей плоскости (Z) с разрезом вдоль положительной части оси x-ов.

Рассмотрим n-таких плоскостей с разрезами:

Первую ветвь будет рассматривать на первом листе, вторую на втором (второй плоскости), …, n-ную ветвь на n-ом листе.

Возьмем какую-нибудь точку на положительной части оси х и отметим ее цифрами. В верхней полуплоскости цифрой 1, на нижние цифрой 2 и т. д. Отметим около нуля окружность, проходящую через отмеченную точку.

Очевидно, при движении Z по окружности из точки 1 в точку 2, аргумент Z возрастает на величину 2π. Следовательно, в рассматриваемой точке получается, что , т. е. ветвь с номером k переходит в ветвь с номером k+1. Значит можно утверждать, что значение ветви 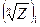в точке 2 будет равно значению ветви в точке 3 и значение в точке 4 и будет равно значению ветви 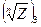в точке 5 и т. д.

Покажем значение n-ной ветви в точке 2π, оно будет равно значению первой ветви в точке 1 ( ) .

Склеим теперь все эти листы следующим образом. Сложим их друг на друга в порядке убывания номеров так, чтобы их разрезы совпали.

Склеим теперь правый берег первого листа с левым берегом второго листа, правый берег второго листа с левым берегом третьего листа и т. д. И наложим правый берег n-ного листа с левым берегом первого листа.

В результате мы получим поверхность Римана для функции W = 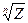. На этой поверхности Римана многозначную функцию W = 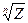можно рассматривать как однозначную функцию.