Теорема. Всякая дробно-линейная (6) с определителем отображает любую прямую или окружность плоскости (Z) на прямую или окружность Г плоскости (W)

Всякая дробно-линейная 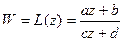(6) с определителем 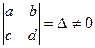отображает любую прямую или окружность плоскости (Z) на прямую или окружность Г плоскости (W). При этом образ Г прямой может быть как прямой, так и окружностью. И аналогично образ Г окружности может быть также как прямой, так и окружность (это круговое свойство).

Доказательство.

Рассмотрим два случая:

1) ;

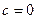2) .

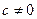1) В случае (1) обязательно 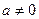и 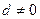, так как определитель 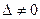. Поэтому в этом случае отображение (6) принимает вид:

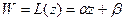(7),

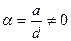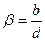, . Очевидно, если число 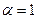, то отображение (7), которое принимает вид (8) является сдвигом плоскости на вектор 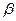плоскости. Такое отображение переводит прямую в прямую, а окружность в окружность.

Пусть 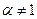, тогда отображение (7) представляет собой произведение двух отображений: растяжения плоскости и поворот. Как известно, каждое из этих отображений переводит прямую в прямую, а окружность в окружность, поэтому и в этом случае отображение (7) обладает круговым свойством (как произведение).

2) Перейдем теперь к рассмотрению случая (2). Предварительно изучим отображения

(9).

Покажем, что отображение (9) обладает круговым свойством. Как известно, общие уравнения прямой и окружности плоскости xy имеют вид

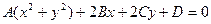(10).

Это будет уравнение прямой, если A = 0, а 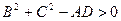. Запишем уравнение (10) в комплексной форме. С этой целью введем обозначения 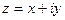, , , 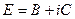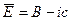. Тогда будет , , 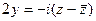. Подставляя эти выражения в равенство (10), мы

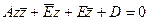(11)

(здесь А и Е вещественные числа, а Е и – сопряженные комплексные числа). В случае прямой, как мы знаем, А = 0 и по крайней мере одно из чисел B и C , что равносильно тому, что 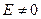. В случае окружности 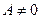, а 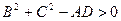, последнее неравенство можно записать так: 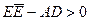. Оказывается, что, если в уравнении (11) вещественное A = 0, а комплексное 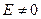, то (11) представляет собой уравнение прямой.

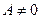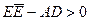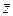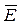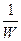Аналогично, если и , то (11) будет уравнением окружности. В этом легко убедиться, если перейти от z, к x и y, а от E и к B и С. Произведем теперь отображение (9) , то есть заменим z на , тогда уравнение (11) преобразуется так ,

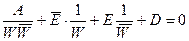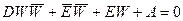(12).

Легко видеть, что уравнение (12) имеет тот же вид, что и уравнение (11), в котором D и A поменялись своими ролями, и Е и поменялись своими ролями. Очевидно, (12) будет уравнением образа прямой или окружности (11) при отображении 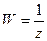. Покажем, что это уравнение является уравнением прямой или окружности.

Возможны два случая 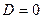и .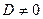

1. Пусть 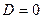. Покажем, что (12) является уравнением прямой. В самом деле, если A = 0, то 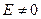и, следовательно, (12) будет уравнением прямой, если же 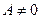и 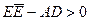, то будет 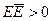и, значит 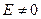. Следовательно, (12) снова является уравнением прямой (так как 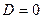, а ).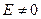

2. Пусть теперь 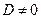. Покажем, что (12) в этом случае является уравнением окружности. Очевидно, нам достаточно доказать, что .

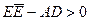Пусть A = 0, тогда 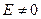и, значит 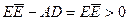. Пусть теперь 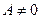и 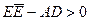, тогда очевидно (12) есть уравнение окружности.

И так отображение 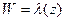является уравнением окружности.

Очевидно, . Введем в рассмотрение отображения , , 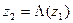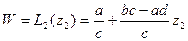. Очевидно коэффициент , (так как 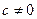, 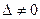). Легко видеть, что отображение 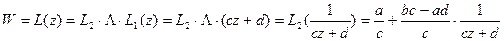. Так как, по доказанному, каждое из отображений 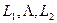обладает круговым свойством, то и их произведение и значит L обладают круговым свойством.

Отметим, что если 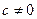, то в точке 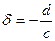значение 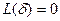. Следовательно, любая прямая или окружность , приходящая через точку 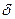обязательно отображается в прямую. Любая же прямая или окружность , не проходящая через точку 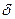, отображается в окружность, так как образ Г линии не будет содержать бесконечно удаленной точки.