Понятие производной функции комплексного переменного

Пусть функция W = f(Z) задана на некотором множестве 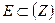и Z₀, принадлежащая E, предельная точка этого множества. Придадим Z₀=x₀+i·y₀ приращение ΔZ = Δx+i·Δy_, чтобы точка Z = Z₀+ΔZ принадлежала множеству Е. Тогда функция W = u+i·v = f(Z) = u(x,y)+i·v(x,y). Получим приращение ΔW = Δu+i·Δv = f(Z₀+ΔZ) - f(Z₀) = Δf(Z₀), .

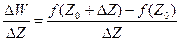Если существует конечный предел 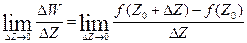, то он называется производной функции f(Z) в точке Z₀ по множеству E, и обозначается 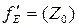, , 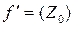, 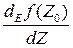W'.

Формально производная функция комплексного переменного определяется точно так же как и производная функции вещественного переменного, но содержание их различно.

В определении производной функции f(x) вещественной переменной в точке х₀ , x → х₀ вдоль прямой. В случае функции комплексного переменного f(Z), Z может стремиться к Z₀ по любому пути плоскости, ведущему в точку Z₀.

Поэтому требование существования производной функции комплексного переменного очень жестко. Этим и объясняется, что даже простые функции комплексного переменного не имеют производной.