Непрерывные кривые

Понятие непрерывной кривой обобщает понятие траектории движущейся точки.

Пусть на некотором отрезке [α,β] задана непрерывная комплексно-значная функция вещественной переменной Z = Z(t) = x(t)+i·y(t) (t принадлежит [α,β]). Будем истолковывать переменную t как время, а значение Z(t) как точку комплексной плоскости. Тогда с изменением времени t от α до β точка Z(t), перемещаясь в комплексной плоскости (Z) опишет некоторую траекторию. Эта траектория и будет непрерывной кривой.

Если задана непрерывная комплексно-значная функция вещественной переменной t (Z = Z(t)) на некотором отрезке [α,β], то говорят, что эта функция определяет в плоскости (Z) непрерывную кривую.

На кривой (Z = Z(t)) можно выбрать два направления. Одно из них соответствует возрастанию t от α до β, а второе убыванию t от β до α.

Точка Z кривой (Z = Z(t)) (t принадлежит [α,β]) называется кратной точкой, если она соответствует не одному, а нескольким значениям параметра t принадлежащего [α,β], одно из которых (по крайней мере) отличается как от α, так и от β.

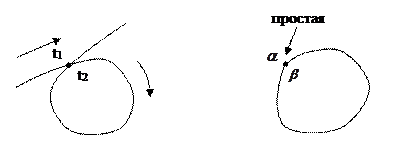
Все точки кривой не являющиеся кратными называются простыми точками кривой.

Кривая, состоящая из одних простых точек, называется простой кривой или кривой Жордана.

Кривая называется замкнутой, если начало и конец ее совпадают, т. е. если Z(α) = Z(β).

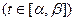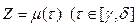Будем считать, что две непрерывные функции Z = λ(t) и ) определяют одну и ту же непрерывную кривую в плоскости (Z), если существует такая монотонная непрерывная функция 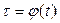, отображающая отрезок [α,β] на [γ,δ], что для любого t принадлежащего [α,β], выполняется равенство λ(t) = μ[φ(t)].

Функция Z = cost , t принадлежит [0,π] определяет непрерывную кривую, совпадающую с отрезком [-1,1].

Рассмотрим теперь кривую Z = cos2t , t принадлежит [0,π], эта кривая геометрически так же совпадает с отрезком [-1,1], однако эта кривая отличается от первой, т. к. она замкнута и состоит из кратных точек, за исключением точки -1, 1. Справедлива теорема Жордана.