Геометрическое истолкование предела последовательности комплексных чисел

Итак, мы знаем модуль разности 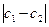представляет собой длину вектора с, начинающегося в точке с₂ и кончающегося в с₁, или расстояние от точки с₂ до с₁.

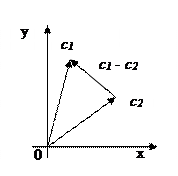
Возьмем произвольные ε > 0 и комплексное число с = a+b·i.

ε-окрестностью точки с комплексной плоскости Z называется внутренность круга радиусом ε с центром в точке c.

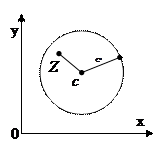
Очевидно, эта окрестность состоит и тех и только тех точек Z плоскости (Z), для которых .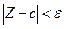

Следовательно, можно дать следующее геометрическое определение предела последовательности комплексных чисел: точка с комплексной плоскости (Z) называется пределом последовательности (с_n), если в любой ε-окрестности точки с содержатся все члены последовательности точек с_n , начиная с некоторого номера ( 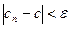n>N)