Геометрический смысл модуля производной

Из определения производной 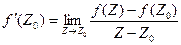, следовательно, (1).

Очевидно, 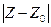– это есть расстояние между точками Z и Z₀, или что тоже – длина вектора . А – это есть расстояние между их образами f(Z) и f(Z₀) или длина вектора f(Z)–f(Z₀). Значит, отношение 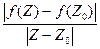можно рассматривать как растяжение вектора с началом в точке Z₀ и концом в точке Z при отображении W = f(Z).

Поэтому, в силу равенства (1), модуль производной 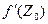можно рассматривать как растяжение в точке 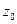при отображении W = f(Z). Очевидно, это растяжение, вообще говоря, не совпадает с отношением 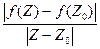, но является его пределом, и это растяжение не зависит от выбора точки .