Амплитудная модуляция

Исторически первым применением амплитудной модуляции явилась задача обеспечения одновременной работы в эфире нескольких радиостанций, передающих сигналы с близкими спектрами (речь, музыка). Суть амплитудной модуляции заключается в переносе полезной информации, заложенной в низкочастотном сообщении, на высокочастотное колебание (несущую частоту). Таким образом, выбирая для каждого сообщения “свою” несущую частоту, можно рассредоточить все сообщения по радиоканалу так, что на приемном конце их легко отличить друг от друга.

Аналогичная задача решается и при одновременной передаче нескольких телефонных переговоров по одному кабелю. Для упрощения анализа рассмотрим амплитудную модуляцию одно-тонального (гармонического) сигнала S(t)=S_mcosW t.

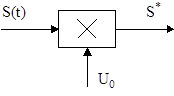Рис. 1.12. Схема амплитуд- ного модулятора на основе перемножителя

В качестве модулятора используем нелинейное устройство - аналоговый перемножитель сигналов, на входы которого подается сигнал S(t), подлежащий модуляции, и опорный сигнал высокой частоты (несущее колебание) U₀=U_mcosw t, w>>W (рис. 1.12). Выходной сигнал модулятора есть продукт перемножения входных сигналов

S^*=aS(t) U₀,

где a - нормирующий множитель с размерностью В^-1, или

S^*=a S(t)U_mcosw t=U_m(t)cosw t (2.3)

Из (2.3) следует, что S^* - это уже высокочастотное колебание, амплитуда которого изменяется пропорционально полезному сигналу S(t). Тем самым информация с низкочастотного исходного сигнала “перенесена” на высокочастотное колебание. Спектр модулированного высокочастотного колебания имеет вид

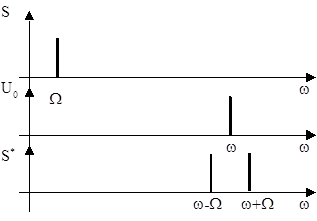Рис. 1.13. Спектры исходного S, несущего U0 и модулированного S* колебания

S^*=a S_mcosW t· U_mcosw t=

=2S_mU_m cos(w - W) t+a S_mU_m cos(w+W) t

и изображен на рис. 1.13, а принцип “рассредоточения” сигналов по каналу связи иллюстрируется на рис. 1.14.

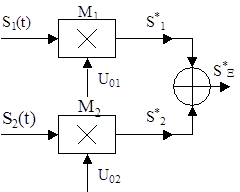
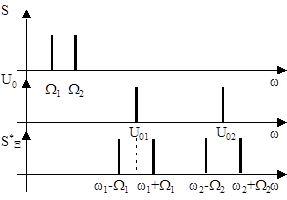Рис. 1.14. Принцип распределения иссле- дования исходных сигналов S1(t), S2(t) с близким спектром по частотному диапа- зону канала связи

На практике амплитудная модуляция чаще всего выполняется за счет воздействия суммы исходного сообщения S(t) и несущего колебания U₀ на нелинейный элемент, характеристика “вход-выход” которого может быть представлена в виде полинома (рис. 1.15)

y=ax+bx²+cx³+...

Легко показать, что квадратичный член полинома может выполнить функцию перемножения, так как

х²=[S(t)+U₀]²=S(t)²+U₀²+2 S(t)U₀.

Не останавливаясь на операции восстановления исходного сообщения S(t), подчеркнем, что она тоже, как и любое другое преобразование спектра, выполняется с помощью нелинейных элементов.