Гармонические и сопряженные гармонические функции

Дважды непрерывно дифференцируемая функция называется гармонической в области D плоскости (Z), если во всех точках этой области выполняется равенство

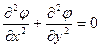(6).

Отметим, что уравнение (6) называют уравнением Лапласа и коротко записывают

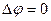(7).

Две функции u(x,y) и v(x,y) области D плоскости (Z) называются сопряженными гармоническими функциями в этой области, если во всех точках этой области выполняются условия Коши-Римана , .

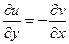Мы покажем, что действительная и мнимая части u(x,y), v(x,y) в аналитической области D функции W = f(Z) являются сопряженными гармоническими функциями. Так как у аналитической функции действительная и мнимая части удовлетворяют условиям Коши-Римана, то нам достаточно доказать гармоничность функций u(x, y), v(x, y) в области D.

Отметим, что аналитическая в области D функция f(Z) имеет производную всех порядков (без доказательства). Поэтому действительная и мнимая части этой функции имеют в области D производные всех порядков по всем переменным, и эти производные непрерывны. Поэтому в частности будут существовать все непрерывные производные 1^го и 2^го порядка. То есть эти функции будут дважды непрерывно дифференцируемы.

Воспользуемся теперь условием Коши-Римана , .

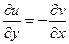Продифференцируем первое равенство по x, а второе – по y, и сложим. Получим 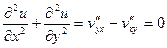(так как смешанные производные, когда непрерывны, равны). Следовательно, u-гармоническая функция, аналогично доказывается, что v гармоническая функция, следовательно, u и v – сопряженные гармонические функции.