Построение мнимой части аналитической функции по ее действительной части
Пусть в некоторой области D плоскости известна действительная часть u(x,y) аналитической функции. Требуется построить ее мнимую часть v(x,y) в этой области. Как мы знаем 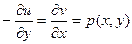 ;
; 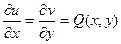 .
.
Составим выражение 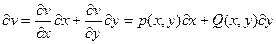 . Очевидно,
. Очевидно, 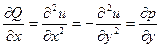 , так как
, так как 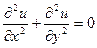 (Лапласиян). Следовательно, выражение
(Лапласиян). Следовательно, выражение 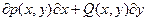 будет полным дифференциалом некоторой функции.
будет полным дифференциалом некоторой функции.
Пусть D – это односвязная область, тогда криволинейный интеграл 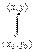
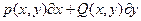 не будет зависеть от формы и пути, соединяющего точки (
не будет зависеть от формы и пути, соединяющего точки ( 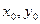 ) и (x,y), принадлежащие D (лежащие в D) и, следовательно, будет представлять собой некоторую функцию
) и (x,y), принадлежащие D (лежащие в D) и, следовательно, будет представлять собой некоторую функцию 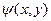 верхнего предела. Как мы знаем из теории криволинейных интегралов, эта функция дифференцируема в области D, и ее частные производные
верхнего предела. Как мы знаем из теории криволинейных интегралов, эта функция дифференцируема в области D, и ее частные производные  и
и 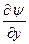 соответственно равны p(x,y), Q(x,y). Следовательно, в области D частные производные функций v(x,y) и
соответственно равны p(x,y), Q(x,y). Следовательно, в области D частные производные функций v(x,y) и 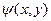 совпадают. Поэтому эти функции могут отличаться лишь на константу, следовательно,
совпадают. Поэтому эти функции могут отличаться лишь на константу, следовательно, 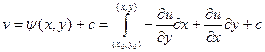 . Как видно, мнимая часть аналитической функции определяется с точностью до постоянной.
. Как видно, мнимая часть аналитической функции определяется с точностью до постоянной.
Отметим, что, если известно значение аналитической функции W = f(Z) в какой-нибудь одной точке 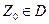 (
( 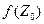 ), то мнимая часть v(x,y) этой функции и, следовательно, сама аналитическая функция f(Z) определяется однозначно по действительной части u(x,y).
), то мнимая часть v(x,y) этой функции и, следовательно, сама аналитическая функция f(Z) определяется однозначно по действительной части u(x,y).
В случае многосвязной области D криволинейный интеграл  представляет многозначную функцию. Поэтому мнимая часть v(x,y) будет также, вообще говоря, многозначной функцией. Действительная часть по мнимой части строится аналогичным образом.
представляет многозначную функцию. Поэтому мнимая часть v(x,y) будет также, вообще говоря, многозначной функцией. Действительная часть по мнимой части строится аналогичным образом.
Отметим, что мнимая часть v(x,y) функции 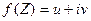 является действительной частью функции
является действительной частью функции  . Отметим, что мнимая часть по действительной находится другим способом. Пишут уравнения
. Отметим, что мнимая часть по действительной находится другим способом. Пишут уравнения 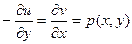 ;
; 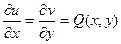 . Интегрируют одно из равенств (первое по x)
. Интегрируют одно из равенств (первое по x)
 (1), затем дифференцируют полученное равенство по переменной y
(1), затем дифференцируют полученное равенство по переменной y 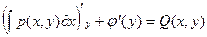 . Отсюда находят
. Отсюда находят 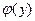 и подставляют его в (1).
и подставляют его в (1).
Пример.
Построить мнимую часть числа по действительной
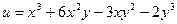 ;
; 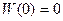
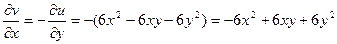
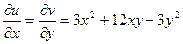 . Интегрируем по x.
. Интегрируем по x.
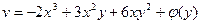 . Находим производную по y и приравниваем
. Находим производную по y и приравниваем
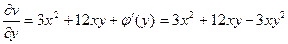
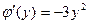 , и теперь интегрируем
, и теперь интегрируем 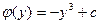 .
.
Таким образом, 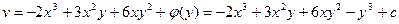
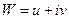 ,
, 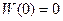 ,
, 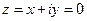
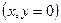 ,
, 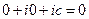 , следовательно,
, следовательно, 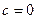 ;
;
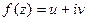
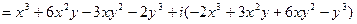 .
.
Дата добавления: 2015-06-12; просмотров: 1908;
