Угол с вершиной в бесконечности или бесконечно удаленная точка

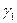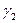Рассмотрим в плоскости (Z) две кривые и , Выходящие из нуля.

Пусть они образуют между собой угол Q в нуле. Произведем отображение 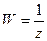. Эти кривые соответственно перейдут в кривые 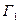и , уходящие в бесконечность.

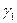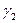Будем считать, что угол между этими кривыми в бесконечности равен углу Q между и с вершиной в нуле.

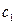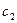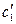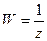Вообще под углом между любыми двумя кривыми и в плоскости (Z) с вершиной в бесконечности мы будем понимать угол между их образами , при отображении с вершиной в нуле.

Покажем, что отображение

W = (2)

конформно и в точке 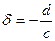. Возьмем любые две кривые 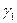и 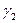плоскости Z, выходящие из точки 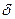и образующие между собой угол Q. Отображение (2) переведет точку 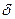в бесконечность, а 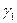и 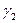в некоторые лини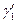и и с вершиной в бесконечности.

Мы покажем, что угол между этими кривыми с вершиной в бесконечности равен Q. Для этого произведем отображение 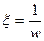, при этом кривые 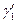и перейдут в некоторые кривые и 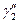плоскости .

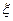Очевидно, угол между и 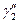с вершиной в нуле, по определению, есть угол между 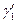и с вершиной в бесконечности. Легко видеть, что кривые и 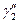получаются из кривых 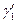, посредством отображения

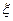= (5).

Так как при отображении (5) точка 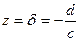переводится в нуль, поэтому по доказанному, отображение (5) будет конформным в точке , и поэтому угол между кривыми , 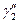с вершиной в нуле будет равен Q. Конформность отображения (2) в точке 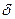установлена.

Аналогичным образом показывается, что отображение (2) конформно и в точке 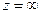. Следовательно, отображение (2) конформно в расширенной плоскости.