Диаграмма состояния. Тройная точка

Если система является однокомпонентной, т. е. состоящей из химически однородного вещества или его соединения, то понятие фазы совпадает с понятием агрегатного состояния. Согласно § 60, одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, при­ходящейся на одну степень свободы ха­отического теплового движения молекул, и наименьшей потенциальной энер­гией взаимодействия молекул может на­ходиться в одном из трех агрегатных состояний: твердом, жидком или газооб­разном. Это соотношение, в свою очередь, определяется внешними условиями - тем­пературой и давлением. Следовательно, фазовые превращения также определяют­ся изменениями температуры и давления. Для наглядного изображения фазовых превращений используется диаграмма со­стояния(рис. 115), на которой в коорди­натах р, Т задается зависимость между температурой фазового перехода и давле­нием в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), раз­деляющих поле диаграммы на три об­ласти, соответствующие условиям су­ществования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Кривые на ди­аграмме называются кривыми фазового равновесия,каждая точка на них соответ-

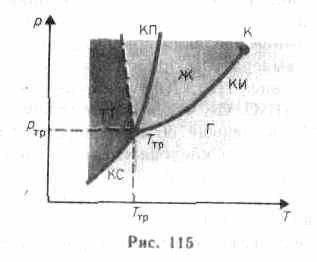
ствует условиям равновесия двух сосуще­ствующих фаз: КП — твердого тела и жидкости, КИ — жидкости и газа, КС — твердого тела и газа.

Точка, в которой пересекаются эти кривые и которая, следовательно, опреде­ляет условия (температуру T_тр и соответ­ствующее ей равновесное давление р_тр) одновременного равновесного сосущество­вания трех фаз вещества, называется тройной точкой.Каждое вещество имеет только одну тройную точку. Тройная точка воды характеризуется температурой 273,16 К (по шкале Цельсия ей соответ­ствует температура 0,01 °С) и является ос­новной реперной точкой для построения термодинамической температурной шкалы.

Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества. Согласно уравнению Кла­пейрона — Клаузиуса,производная от равновесного давления по температуре

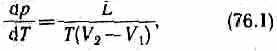
где L — теплота фазового перехода, (V₂-V₁)—изменение объема вещества при переходе его из первой фазы во вто­рую, Т — температура перехода (процесс изотермический).

Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равновесия. Поскольку L и Т положитель­ны, наклон задается знаком V₂-V₁. При испарении жидкостей и сублимации твер­дых тел объем вещества всегда возраста­ет, поэтому, согласно (76.1), dp/dT>0; следовательно, в этих процессах повыше­ние температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. dp/dT>0; следовательно, увеличение давления приводит к повыше­нию температуры плавления (сплошная КП на рис. 115). Для некоторых же ве­ществ (H₂O, Ge, чугун и др.) объем жид­кой фазы меньше объема твердой фазы, т. е. dp/dT<0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая ли­ния на рис. 115).

Диаграмма состояния, строящаяся на

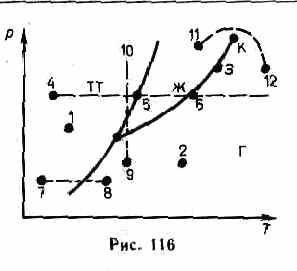
основе экспериментальных данных, позво­ляет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствую­щих точке 1 (рис. 116), вещество находит­ся в твердом состоянии, точке 2 — в газо­образном, а точке 3 — одновременно в жидком и газообразном состояниях. До­пустим, что вещество в твердом состоянии, соответствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграмме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствую­щей точке 5, вещество плавится, при более высокой температуре, соответствующей точке 6,— начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жид­кость — кристаллическое состояние.

На диаграмме состояний (см. рис. 115 и 116) видно, что кривая испарения заканчивается в критической точке К. По­этому возможен непрерывный переход ве­щества из жидкого состояния в газообраз­ное и обратно в обход критической точки, без пересечения кривой испарения (пере­ход 11—12 на рис. 116), т. е. такой пере­ход, который не сопровождается фазовы­ми превращениями. Это возможно благо­даря тому, что различие между газом и жидкостью является чисто количествен-

ным (оба эти состояния, например, явля­ются изотропными). Переход же кристал­лического состояния (характеризуется анизотропией) в жидкое или газообразное может быть только скачкообразным (в ре­зультате фазового перехода), поэтому

кривые плавления и сублимации не могут обрываться, как это имеет место для кри­вой испарения в критической точке. Кри­вая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р=0 и Т=0.

Контрольные вопросы

•Чем отличаются реальные газы от идеальных? Каков смысл поправок при выводе уравнения Ван-дер-Ваальса?

• Почему перегретая жидкость и пересыщенный пар являются метастабильными состояниями? При адиабатическом расширении газа в вакуум его внутренняя энергия не меняется. Как изме­нится температура, если газ идеальный? реальный?

• Каковы суть и причины эффекта Джоуля — Томсона? Когда его называют положительным? отрицательным?

• Почему у всех веществ поверхностное натяжение уменьшается с температурой? Что представляют собой поверхностно-активные вещества? При каком условии жидкость смачивает твердое тело? не смачивает? От чего зависит высота поднятия смачивающей жидкости в капилляре? Чем отличаются монокристаллы от поликристаллов? Как можно классифицировать кристаллы?

• Как получить закон Дюлонга и Пти исходя из классической теории теплоемкости? Некоторое количество твердого вещества смешано с тем же веществом в жидком состоянии. Почему при некотором нагреве этой смеси ее температура не поднимается? Чем отличается фазовый переход I рода от фазового перехода II рола?

• Что можно «вычитать» из диаграммы состояния, используемой для изображения фазовых превращений?

Задачи

10.1.Углекислый газ массой m=1 кг находится при температуре 290 К в сосуде вместимостью 20 л. Определить давление газа, если: 1) газ реальный; 2) газ идеальный. Объяснить разли­чие в результатах. Поправки а и b принять равными соответственно 0,365 Н•м⁴/моль² и 4,3•10^-5 м³/моль. [ 1) 2,44 МПа; 2) 2,76 МПа ]

10.2.Кислород, содержащий количество вещества v = 2 моль, занимает объем V₁ = 1 л. Опреде­лить изменение DT температуры кислорода, если он адиабатически расширяется в вакуум до объема V₂=10 л. Поправку а принять равной 0,136 Н•м⁴/моль². [-11,8 К |

10.3.Показать, что эффект Джоуля — Томсона всегда отрицателен, если дросселируется газ, для которого силами притяжения молекул можно пренебречь.

10.4.Считая процесс образования мыльного пузыря изотермическим, определить работу А, кото­рую надо совершить, чтобы увеличить его диаметр от d₁=2 см до d₂=6 см. Поверхностное натяжение о мыльного раствора принять равным 40 мН/м. [0,8 мДж |

10.5.Воздушный пузырек диаметром d=0,02 мм находится на глубине А=20 см под поверхностью воды. Определить давление воздуха в этом пузырьке. Атмосферное давление принять нор­мальным. Поверхностное натяжение воды s=73 мН/м, а ее плотность r=1 г/см³ [ 118 кПа |

10.6.Вертикальный открытый капилляр внутренним диаметром d = 3 мм опущен в сосуд с ртутью. Определить радиус кривизны ртутного мениска в капилляре, если разность уровней ртути в сосуде и в капилляре Dh=3,7 мм. Плотность ртути r= 13,6 г/см³, а поверхностное натяже­ние а = 0,5 Н/м. [ 2 мм ]

10.7.Для нагревания металлического шарика массой 25 г от 10 до 30 °С затратили количество теплоты, равное 117 Дж. Определить теплоемкость шарика из закона Дюлонга и Пти и мате­риал шарика. [М»107 кг/моль; серебро]