Элементарные аналитические функции
Среди аналитических функций наиболее простыми являются целые функции.
Функция W = f(Z) называется целой, если она является аналитической в конечной комплексной плоскости.
Многочленом степени n называется функция вида 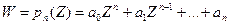 (
( 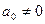 ). Это есть целая функция, так как она всюду имеет производные.
). Это есть целая функция, так как она всюду имеет производные.
Очевидно, при 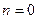
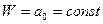 .
.
Мы будем рассматривать случай, когда 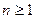 (
(  – комплексные числа,
– комплексные числа, 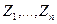 – комплексные переменные).
– комплексные переменные).
Очевидно, 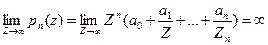 . Поэтому можно считать, что
. Поэтому можно считать, что 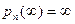 . Как известно из алгебры, при любом W уравнение
. Как известно из алгебры, при любом W уравнение  имеет n корней в комплексной плоскости, при чем некоторые из них могут быть кратные. Следовательно, Любая точка W комплексной плоскости (W) принадлежит образу плоскости (Z) при отображении
имеет n корней в комплексной плоскости, при чем некоторые из них могут быть кратные. Следовательно, Любая точка W комплексной плоскости (W) принадлежит образу плоскости (Z) при отображении 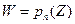 (
( 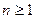 ).
).
Так как 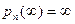 , рассмотренная комплексная плоскость (Z) отображается на расширенную комплексную плоскость (W). При этом каждой точке
, рассмотренная комплексная плоскость (Z) отображается на расширенную комплексную плоскость (W). При этом каждой точке 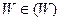 , за исключением некоторого конечного числа точек, имеет в плоскости (Z) ровно n прообразов
, за исключением некоторого конечного числа точек, имеет в плоскости (Z) ровно n прообразов 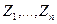 . Найдем те исключительные W плоскости (W), которые имеют в плоскости (Z) меньше, чем n прообразов. Очевидно, к этим точкам относятся точки
. Найдем те исключительные W плоскости (W), которые имеют в плоскости (Z) меньше, чем n прообразов. Очевидно, к этим точкам относятся точки 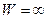 , у нее в плоскости (Z) один прообраз
, у нее в плоскости (Z) один прообраз 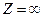 . Мы будем считать, что эта точка
. Мы будем считать, что эта точка 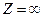 является и кратной точкой. Будем считать, что
является и кратной точкой. Будем считать, что 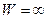 , так как точка W при отображении
, так как точка W при отображении 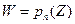 имеет в плоскости (Z) меньше, чем n прообразов, то, по крайней мере, один из них является кратным. Обозначим его через
имеет в плоскости (Z) меньше, чем n прообразов, то, по крайней мере, один из них является кратным. Обозначим его через  Z0. Как известно, кратный корень уравнения
Z0. Как известно, кратный корень уравнения  является так же корнем уравнения
является так же корнем уравнения 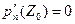 . Производная
. Производная 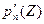 имеет уже степень n-1, поэтому уравнение
имеет уже степень n-1, поэтому уравнение  будет иметь не более чем n-1 различных корней. Обозначим их через
будет иметь не более чем n-1 различных корней. Обозначим их через  , тогда точки
, тогда точки 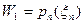 ,…,
,…, 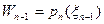 и
и 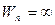 будут иметь в плоскости (Z) меньше, чем n прообразов.
будут иметь в плоскости (Z) меньше, чем n прообразов.
Дата добавления: 2015-06-12; просмотров: 1388;
