Пример (дробно-линейная функция)
Функция вида W = f(z)=  (2) называется дробно-линейной функцией (здесь a, b, c, d – фиксированные комплексные числа, а z – комплексная переменная).
(2) называется дробно-линейной функцией (здесь a, b, c, d – фиксированные комплексные числа, а z – комплексная переменная).
Мы будем рассматривать случай, когда  (3).
(3).
Очевидно, в случае 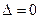 строки определителя пропорциональны.
строки определителя пропорциональны.
Пусть 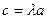 ,
, 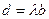
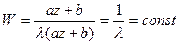 и этот случай не интересен, так как вся плоскость переводится в одну точку.
и этот случай не интересен, так как вся плоскость переводится в одну точку.
Очевидно, выполняется, по крайней мере, одно из условий:
а) с = 0;
б) с ≠ 0.
а) Рассмотрим случай с = 0, так как 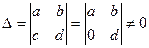 , то обязательно a и d не равны нулю. Положим
, то обязательно a и d не равны нулю. Положим  ,
, 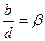 , тогда отображение (2) запишется в виде
, тогда отображение (2) запишется в виде 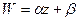 ,
, 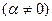 (4).
(4).
Очевидно производная 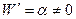 , поэтому отображение (4) конформно в любой точке плоскости (Z). При этом отображении угол поворота касательной к кривым постоянен во всех точках плоскости (Z) и равен
, поэтому отображение (4) конформно в любой точке плоскости (Z). При этом отображении угол поворота касательной к кривым постоянен во всех точках плоскости (Z) и равен 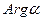 . Растяжение также во всех точках будет фиксировано и будет равно
. Растяжение также во всех точках будет фиксировано и будет равно 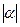 . Очевидно, если
. Очевидно, если 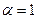 , то
, то  ,
, 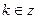 и
и  .
.
Следовательно, в этом случае отсутствует поворот и растяжение.
Отображение 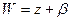 осуществляет при этом сдвиг всей плоскости на вектор
осуществляет при этом сдвиг всей плоскости на вектор 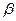 .
.
Пусть теперь 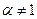 . Тогда отображение (4) можно переписать так
. Тогда отображение (4) можно переписать так 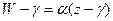 , где
, где 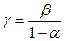 . Отсюда видно, что
. Отсюда видно, что 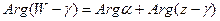 и
и  .
.

Таким образом, в данном случае при отображении (4) векторы 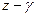 , выходящие из точки
, выходящие из точки  , растягиваются в
, растягиваются в 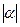 раз и затем поворачиваются на угол
раз и затем поворачиваются на угол 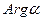 . Следовательно, при этом отображении вся плоскость относительно точек
. Следовательно, при этом отображении вся плоскость относительно точек  растягивается в
растягивается в 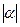 раз и затем поворачивается на угол
раз и затем поворачивается на угол 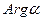 .
.
б) Пусть теперь с 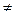 0. Очевидно,
0. Очевидно, 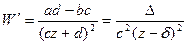 , где
, где 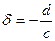 , число
, число  . Нетрудно видеть, что производная
. Нетрудно видеть, что производная 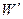 конечна и отлична от нуля во всех точках
конечна и отлична от нуля во всех точках 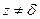 , поэтому
, поэтому 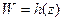 является конформным во всех точках
является конформным во всех точках 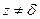 . При этом отображении касательные к кривым поворачиваются на угол
. При этом отображении касательные к кривым поворачиваются на угол 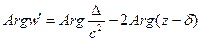 . Растяжение во всех точках будет равно
. Растяжение во всех точках будет равно 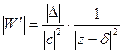 .
.
Из этих формул непосредственно видно, что поворот касательных к кривым будет одним и тем же в тех точках  , где
, где  сохраняет постоянное значение. Очевидно, это будут лучи
сохраняет постоянное значение. Очевидно, это будут лучи 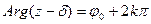 , исходящие из точек
, исходящие из точек 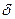 . Растяжение будет одним и тем же только в точках
. Растяжение будет одним и тем же только в точках  , где
, где 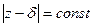 , то есть на окружностях с центром в точке
, то есть на окружностях с центром в точке 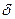 .
.
Дата добавления: 2015-06-12; просмотров: 821;
