Геометрический смысл аргумента производной комплексной функции
Пусть функция W = f(Z) имеет в точке 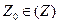 конечную производную
конечную производную 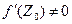 , вычислим геометрический смысл
, вычислим геометрический смысл 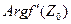 . С этой целью выпустим из точки
. С этой целью выпустим из точки 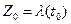 кривую
кривую 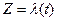 , такую что производная
, такую что производная 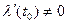 и существует.
и существует.

Отображение W=f(Z) переведет эту кривую L в новую кривую 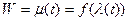 , выходящую из точки
, выходящую из точки 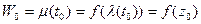 (T и
(T и 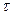 касательные).
касательные).
Покажем, что кривая 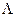 (лямбда), заданная уравнением
(лямбда), заданная уравнением 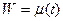 тоже имеет в точке
тоже имеет в точке 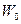 касательную. Очевидно,
касательную. Очевидно, 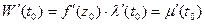 , значит
, значит 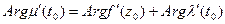 (3).
(3).
Таким образом, кривая 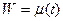 имеет в точке
имеет в точке 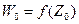 касательную, которая составляет с действительной осью угол равный величине (3). Из равенства (3) следует, что
касательную, которая составляет с действительной осью угол равный величине (3). Из равенства (3) следует, что
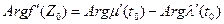 (4).
(4).
Следовательно, 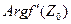 – это есть угол, на который поворачивается касательная к кривой L в рассматриваемой точке Z0 при отображении W=f(Z). Нетрудно видеть, что угол поворота касательной к кривой
– это есть угол, на который поворачивается касательная к кривой L в рассматриваемой точке Z0 при отображении W=f(Z). Нетрудно видеть, что угол поворота касательной к кривой 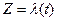 в точке Z0 при отображении W = f(Z) не зависит от выбора этой кривой.
в точке Z0 при отображении W = f(Z) не зависит от выбора этой кривой.
Если мы возьмем в плоскости (Z) две кривые  и
и  , образующие в точке Z0 некоторый угол Q.
, образующие в точке Z0 некоторый угол Q.

То при отображении W = f(Z) эти две кривые перейдут в новые кривые 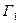 и
и 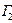 плоскости (W), которые в точке
плоскости (W), которые в точке 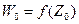 также будут образовывать угол Q, так как касательные к
также будут образовывать угол Q, так как касательные к 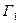 и
и 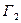 в точке
в точке 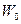 получаются путем поворота касательных к
получаются путем поворота касательных к  и
и  в точке
в точке 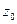 на один и тот же угол, равный
на один и тот же угол, равный 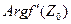 .
.
Дата добавления: 2015-06-12; просмотров: 943;
