Геометрический смысл аргумента комплексно-значимой функции вещественной переменной

Рассмотрим комплексно-значимую функцию вещественной переменной 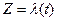, 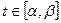. Пусть эта функция в некоторой точке 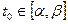имеет производную 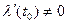(так как аргумент 0 и 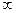не определен).

Выясним геометрический смысл аргумента .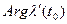

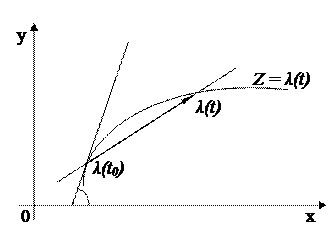
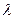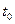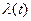Рассмотрим в плоскости (Z) две точки ( ) и на кривой 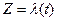. Проведем

через эти две точки секущую. Очевидно, вектор 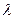( 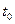)– 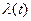коллинеарен этой секущей. Значит, отношение 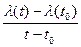так же этот вектор будет коллинеарен секущей. Вычислим предел, 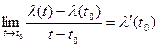, поэтому

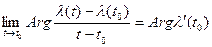(2)

(Этот предел не в обычном смысле, то есть из 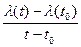можно извлечь такие представители, которые будут сходится к одному из представителей ).

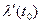Так как касательная – это есть предельное положение секущей, то из равенства (2) следует, что 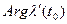– это есть угол, который составляет касательная к кривой 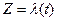в точке 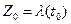с действительной осью.