Примеры. 1°. Найти базис, взаимный к базису: е1(1, 1, 0), е2(1, 0, 1), е3(0, 1, 1).

1°. Найти базис, взаимный к базису: е₁(1, 1, 0), е₂(1, 0, 1), е₃(0, 1, 1).

◀ а) Строим матрицу: . Получаем: ;

.

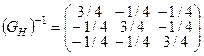б) Составляем матрицу ;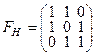

в) и находим: .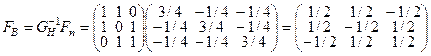

г) Строки полученной матрицы F_B и есть векторы взаимного базиса, т.е.

е¹(1/2, 1/2, –1/2), е²(1/2, –1/2, 1/2), е³(–1/2, 1/2, 1/2) ▶

2°.Найдем базис взаимный к базису: е¹(1, 1, 1), е²(0, 1, 1), е³(0, 0, 1).

◀ Строим матрицу: 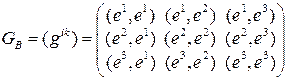, т.е. 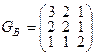; 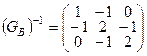. Находим .

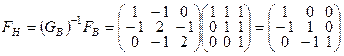Таким образом найдены векторы взаимного базиса: е₁(1, 0, 0), е₂(–1, 1, 0), е₃(0, –1, 1) ▶

Задача 2. Вектор х (5, 2, 1) задан своими координатами в том же базисе, в котором заданы векторы двух взаимных базисов: е₁(1, 1, 0), е₂(1, 0, 1), е₃(0, 1, 1) и е¹(1/2, 1/2, –1/2), е²(1/2, –1/2, 1/2), е³(–1/2, 1/2, 1/2). Найти ковариантные и контравариантные координаты вектора х в базисе {e₁, e₂, e₃, e¹, e², e³}.

◀ Вектор x = (xe_i)eⁱ = 7e¹ + 6e² + 3e³ поэтому (х₁, х₂, х₃) = (7, 6, 3) – ковариантные координаты х.

Вектор x = (xeⁱ)e_i = 3e₁ + 2e₂ – e₃, следовательно (х¹, х², х³) = (3, 2, –1) – контравариантные координаты х ▶