Е1(1/2, 1/2, –1/2) « е1¢(1, 1, 1) .

е²(1/2, –1/2, 1/2) е^2¢(0, 1, 1)

е³(–1/2, 1/2, 1/2) е^3¢(0, 0, 1)

Строим матрицу 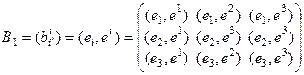. Имеем ;

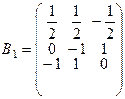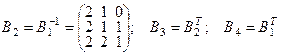. Чтобы проверить формулу 1) 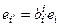мы должны матрицу В₁ умножить на матрицу у которой в строках стоят e_i – получим матрицу у которой в строках e_i¢, аналогично проверяются формулы 2), 3), 4).

1) ;

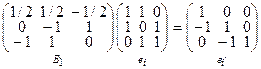2) ;

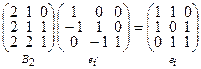3) ;

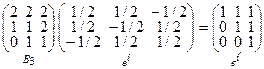4) ▶

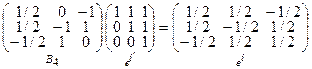Информация к размышлению:

Та же задача: В базисе, в котором заданы координаты всех векторов, построить матрицу перехода от базиса {e_i} к базису {e_i¢} (а также от базиса {eⁱ} к базису {e^i¢}).

◀ а) пусть P_S®e – матрица перехода из стандартного базиса в базис {е_i}, т.е. для построения матрицы P_S®e координаты векторов e_i пишутся в столбцы;

б) P_е®S = (P_S®e)^–1;

в) P_S®e¢ – матрица перехода из стандартного базиса в базис {e_i¢} ;

г) P_е®e¢ = (P_S®e¢)(P_S®e)^–1 ▶

Примеры:

1°. е₁(1, 1, 0) е_1¢(1, 0, 0)

е₂(1, 0, 1) е_2¢(–1, 1, 0)