Понятие тензора

Пусть V – вещественное (не обязательно евклидово) линейное пространство (dimV = n).

Def:Тензором типа (p, q) , (p раз ковариантным, q раз контравариантным) называется геометрический объект, который:

1)в любом базисе {e_i} линейного пространства V_n определяется n^p+q координатами 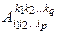(индексы принимают значения 1, 2, …, n каждый);

2)обладает свойством, что его координаты 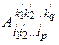в базисе {e_i¢} связаны с координатами 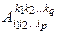в базисе {e_i} соотношениями:

; (*)

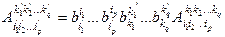и здесь 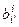элементы матрицы перехода от старого базиса к новому (e_i ® e_i¢), а 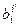– элементы матрицы обратного перехода.

Число r = p + q называется рангом тензора.

Формула (*) называется формулой преобразования тензора при изменении базиса.

Замечание:Индексы i₁i₂ … i_p называются ковариантными, а k₁k₂ … k_q – контравариантными.

Отметим:Ковариантные и контравариантные координаты вектора преобразуется по формуле (*) (p = 1, q = 0 для ковариантных координат, p = 0, q = 1 для контравариантных координат).

Поэтому вектор представляет собой тензор первого ранга (1 раз ковариантный, либо 1 раз контравариантный – в зависимости от выбора типа координат этого вектора).

Отметим: Скаляр – тензор нулевого ранга – имеет одну координату, причем не имеющую индексов и не изменяющуюся при изменении системы координат.

Замечание: Нетрудно убедиться в том, что последовательный переход от {e_i} к {e_i¢}, а затем от {e_i¢} к { 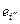}, приводит к тем же результатам, что непосредственный переход от {e_i} к { 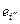} , т.е. определение тензора корректно.

Замечание:Любая системаn^p+q чисел 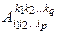может в данном базисе 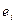рассматриваться как координаты некоторого тензора А типа (p, q).