Афинные ортогональные тензоры

Пусть 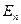— эвклидово пространство и { 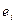} его ортонормированный базис. Если поставить задачу нахождения базиса { 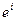} взаимного к базису { 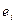}, то нетрудно видеть что ортонормированный базис взаимен самому себе: = .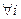

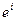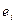Тогда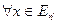

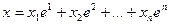
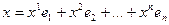
Следовательно получим, что .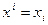

Т.е. в ортонормированном базисе ковариантные и контравариантные координаты вектора x совпадают.

При этом можно записать:

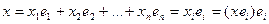
В ортонормированном базисе вместо формул Гиббса имеем формулу: .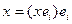

Рассмотрим переход от одного ортонормированного базиса { 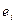} к другому ортонормированному базису { }.

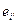Формулы преобразования для произвольных базисов имели вид:

; ;

; ;

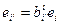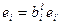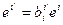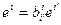Обозначая 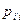элементы матрицы Р перехода от базиса { 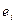} к базису { 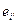} можно указанные формулы переписать в виде:

= ; = ;

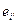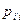
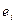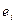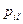
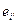умножая скалярно первое равенство на 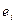, а второе на 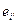получим:

=( , )=( , )= ;

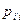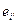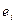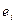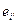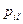Т.е. для матрицы перехода Р справедливо соотношение P^-1=P^T или то же самое: PP^T=P^TP

следовательно матрица оператора перехода ортогональна.

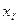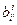
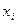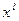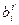
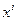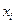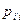
Формулы для преобразования ковариантных и контравариантных координат вектора x имели вид: = и = . В случае ортонормированных базисов они будут иметь вид: = 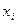и = ,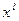

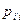
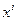Т.е. и ковариантные и контравариантные координаты преобразуются с помощью одной и той же матрицы перехода Р от базиса { 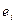} к базису { 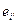}, т.е.согласованно с базисными векторами. В силу этого для ортонормированных базисов все координаты векторов ковариантны и преобразуются по одному и тому же закону: = .

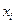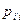
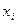В дальнейшем, в соответствии с выше сказанным, в ортонормированных базисах (т.е. при ортогональных преобразованиях) все координаты будут ковариантны, т.е. все индексы нижние.

И наконец:

Def: Аффинным ортогональным тензором А ранга r называется объект, который :

1) В каждом ортонормированном базисе { 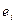} евклидова пространства 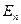определяется 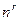координатами 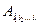(индексы принимают значения от1 до n).

2) Обладает свойством, что его координаты 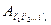в другом ортонормированном базисе { 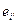} связаны с координатами 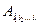в ортонормированном базисе { 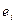} соотношениями:

= …

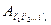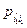
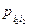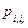
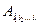
В дальнейшем изложение будет вестись для аффинных ортогональных тензоров, и для простоты, в дальнейшем именно их будем именовать словом: тензор.

§8. Операции над аффинными ортогональными

тензорами

Отношение равенства тензоров, операции сложения, вычитания и умножения тензоров на число определяются как операции покоординатного равенства, сложения, вычитания и умножения на число в некотором базисе. Умножение и свёртка тензоров производится, как и в случае тензоров общего вида, но при свёртке отмечается не один верхний и один нижний индексы а, естественно, два нижних.

Свёртка тензора 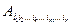по индексам 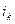и 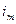это фактически умножение на тензор 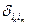(Здесь 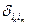тензор Кронекера).

Скалярное произведение тензоров. Часто в тензорной алгебре применяется комбинация операций умножения тензоров с последующей свёрткой по паре индексов. При этом ранг результирующего тензора будет равен ( 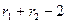), где 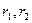- ранги перемножаемых тензоров.

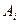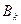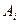
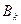
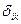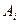
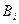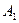
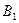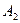
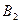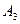
В частности для тензоров первого ранга (векторов) и получаем: = = + + 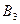, а это просто скалярное произведение двух векторов.

По аналогии с этим простейшим случаем, комбинацию перемножения тензоров с последующей свёрткой называют скалярным или внутренним произведением тензоров.