Еще раз о свойствах симметрии тензоров
Def: Если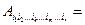 
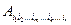, то тензор 
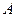называется симметричным по индексам 
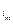и 
.
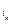Если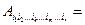 
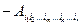, то тензор 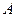называется антисимметричным (или кососимметричным ) по индексам 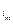и .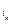
1º Симметрия и антисимметрия тензоров инвариантна относительно преобразования системы координат.
◀ (На примере тензора ранга 2)
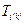
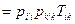
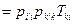
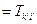- симметричность
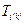
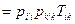
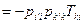
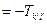- антисимметричность. ▶
В пространстве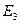 
(размерности 3) антисимметричный и симметричный тензоры 2-го ранга имеют вид: 
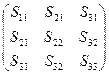и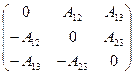 
, т.е. симметричный тензор имеет только шесть независимых переменных, а антисимметричный и вовсе три независимых переменных.
Это дает возможность предложить следующую геометрическую интерпретацию симметричного и антисимметричного тензоров 2-го ранга в пространстве размерности 3:
2º. Каждому антисимметричному тензору 2-го ранга может быть поставлен в соответствие вектор и наоборот, каждый вектор связан с некоторым антисимметричным тензором 2-го ранга.
3º Любому не нулевому симметричному тензору 2-го ранга соответствует некоторая, и притом, единственная поверхность второго порядка определяемая уравнением: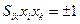 
( 
).
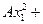
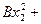
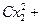
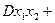
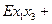
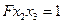4º Произведение симметрического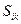 
и антисимметрического 
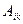тензоров 2-го ранга с последующим двукратным свертыванием равно 0.
◀ Действительно :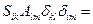 
,
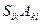Из симметрии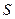 
: 
,
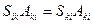индексы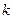 
и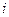 
немые, поэтому 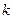обозначим 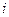, а 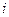обозначим : 
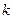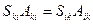
Из антисимметрии :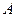 
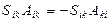, Т.е. 
. ▶
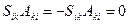5º Любой тензор второго ранга может быть представлен в виде суммы симметричного и антисимметричного тензоров, т.е.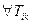 
- тензора 2-го ранга
◀ 
. ▶
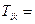
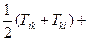
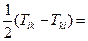
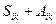Дата добавления: 2015-05-05; просмотров: 1056;