Оператора и с определителями

Пусть в Е_n задан линейный оператор А с матрицей (а_ij). Тогда: y_i = a_ijx_j (в базисе е_i). Рассмотрим в Е_n базис {e_i¢}: y_i¢ = a_i¢j¢x_j¢ Þ p_i¢iy_i = a_i¢j¢p_j¢jx_j . Умножим обе части равенства на p_i¢k. p_i¢ip_i¢ky_i = a_i¢j¢p_j¢jp_i¢kx_j Þ d_iky_i = a_i¢j¢p_j¢jp_i¢kx_j Þ y_k = p_i¢kp_j¢ja_i¢j¢x_j. С другой стороны: y_i = a_ijx_j, т.е. a_ij = p_i¢ip_j¢ja_ij.

Таким образом, элементы матрицы линейного оператора образуют тензор 2^го ранга.

Наоборот всякий тензор 2^го ранга можно истолковать как матрицу линейного оператора.

Поэтому теория тензоров 2^го ранга непосредственно связана с теорией линейных операторов и с теорией матриц.

Это дает возможность выявить связь тензоров 2^го ранга с определителями и т.д.

Теперь: пусть j_ik – произвольный тензор 2^го ранга. Построим тензор 3^го ранга c_abc по правилу: c_abc = e_iklj_iaj_kbj_lc . Тогда c_bac = e_iklj_ibj_kaj_lc 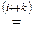e_kilj_kbj_iaj_lc = e_kilj_iaj_kbj_lc = =-e_iklj_iaj_kbj_lc = –c_abc. Следовательно абсолютно антисимметричный тензор 3^го ранга всегда можно представить в виде: c_abc = je_abc, где φ – скаляр. Т.е. каждому тензору 2^го ранга φ_ik можно поставить в соответствие скаляр φ такой, что:

e_iklj_iаj_kbj_lc = je_abc (*)

Оказывается, что этот скаляр равен определителю, составленному из компонент φ_ik: , в этом легко убедиться непосредственным вычислением, например, зафиксировав в (*) говорящие индексы (скажем а = 1, b = 2, c = 3) и выполнив суммирование по немым индексам i, k, l: je₁₂₃ = e_iklj_i1j_k2j_l3 = …

В этой же идеологии нетрудно ввести понятия тензора обратного к данному тензору 2^го ранга (Если , то тензор 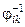обратный к тензору j_ik), и получить условия обратимости тензора 2^го ранга.

Можно сформулировать (а для симметричного тензора и всегда решить) задачу о приведении тензора 2^го ранга к главным осям. Эта задача равносильна задаче построения собственного базиса для линейного оператора.