По координатам точки пространства
Пусть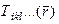 
– тензорное поле rго ранга. Каждую из 3r компонент этого поля продифференцируем по каждой из трех координат x1, x2, x3. Получим совокупность 3r+1 функций вида 
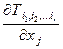(j = 1, 2, 3).
Тº. Если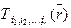 
– тензорное поле ранга r, то 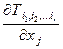будет тензорным полем ранга (r + 1).
◀ Отметим что, если xi = pii¢ 
то 
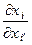= pii¢ = 
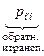, и следовательно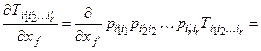 
▶
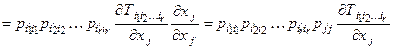Итак, дифференцирование тензорного поля по координатам повышает ранг тензорного поля на единицу.
В частности, применение этой операции к скалярному полю φ порождает векторное поле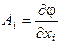 
, которое называется градиентом скалярного поля.
По аналогии с градиентом скалярного поля, тензорное поле 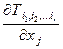(j = 1, 2, 3) называют градиентом тензорного поля ранга r.
Дата добавления: 2015-05-05; просмотров: 764;