Корень m-й степени из оператора
Def: Эрмитов оператор А называется положительным, если "хÎV, (Ax, x) ³ 0. Если, кроме того, из (Ax, x) = 0 Þ x = 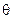 , то А называют положительно определенным оператором (Обозначается: A ³ 0, A > 0 соответственно).
, то А называют положительно определенным оператором (Обозначается: A ³ 0, A > 0 соответственно).
Тº. Каждое собственное значение положительного (положительно определенного)
оператора неотрицательно (положительно).
◀ Если λ – собственное значение А, то $x такой, что ||x|| = 1, (Ax, x) = l (было доказано), отсюда следует утверждение теоремы ▶
Def: Корнем m-й степени из оператора А называется такой оператор В, что Вm = A.
Тº. Если А – положительный эрмитов оператор (А ³ 0), то "mÎN существует
положительный эрмитов оператор 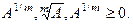
◀ Пусть lk - собственные значения А (k =1, 2, 3,…, n) и {ek} - ортонормированный собственный базис, 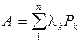 (спектральное разложение) и при этом lk ³ 0. Рассмотрим оператор
(спектральное разложение) и при этом lk ³ 0. Рассмотрим оператор 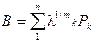 . Изучим свойства оператора В. Оператор В:
. Изучим свойства оператора В. Оператор В:
а) эрмитов: 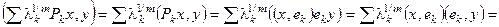
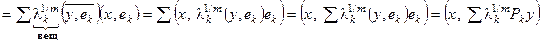 ;
;
б) положителен: 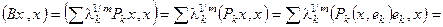
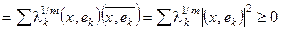 ;
;
в) 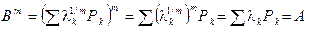 . Теорема доказана. ▶
. Теорема доказана. ▶
Примечание: В ортонормированном базисе {ek} из собственных векторов матрица оператора А и матрица А1/m имеют вид: 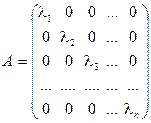 ,
,
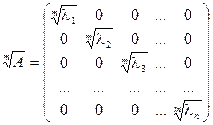 .
.
Дата добавления: 2015-05-05; просмотров: 1003;
