Квадратичные формы в унитарном пространстве

Def: Квадратичной формой называют В(х, х), соответствующую полуторалинейной форме В(х, у).

Тº. Пусть В(х, у) – эрмитова форма в n-мерном унитарном пространстве V. Тогда в V

существует ортонормированный базис {e_k} и существуют вещественные числа λ_k,

что для "хÎV в базисе {e_k}: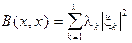

◀ В(х, у) – эрмитова Þ В(х, у) = (Aх, у), где А – эрмитов оператор. А – эрмитов Þ ${e_k} – собственный ортонормированный базис и λ_k – собственные числа оператора А

; .

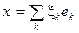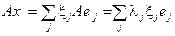Тогда: ▶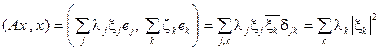

И еще одна теорема: о приведении пары квадратичных форм к каноническому виду:

Тº. Пусть А(х, у) и В(х, у) – эрмитовы формы в линейном пространстве V и, кроме

того, "хÎV, х ¹ q, В(х, у) > 0. Тогда в V существует базис {e_k}, в котором:

.

◀ В(х, у) – эрмитова, В(х, у) > 0, "хÎV, х ¹ q. Из этих условий: В линейном пространстве V можно ввести скалярное произведение векторов х и у по правилу: (х, у) = В(х, у).

После введения скалярного произведения пространство V станет унитарным и в нем, согласно предыдущей теореме, существует ортонормированный базис {e_k} и числа λ_k, что в этом базисе .

С другой стороны, так как базис ортонормированный, то 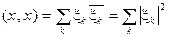и

В(х, х) = (х, х), т.е. В(х, х) = ▶