Нормальная жорданова форма

Пусть А – линейный оператор, действующий в комплексном векторном пространстве V. Если в V существует базис {e_k} из собственных векторов оператора А, то в этом базисе матрица оператора А имеет диагональный вид 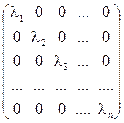, где λ – соответствующие собственные значения оператора А.

Так будет, например, в том случае, когда характеристичное уравнение оператора А: det(A – lЕ) = 0 имеет n попарно различных корней.

Однако это далеко не всегда так. Например, оператор А с матрицей А = 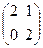имеет характеристическое уравнение: j(l) = (2 - l)² = 0. Это уравнение имеет кратный корень λ = 2 и этому корню соответствует лишь один собственный вектор (1, 0) (или ему коллинеарные). И матрица оператора А ни в каком базисе не приводится к диагональному виду.

Поэтому возникает вопрос, о каком-то другом, достаточно простом виде, к которому можно привести матрицу всякого линейного оператора.

В комплексном пространстве таким «простейшим», каноническим видом принято считать так называемую жорданову форму матрицы.

Def: Жордановой клеткой G_k(λ) называется квадратная матрица k-го порядка вида:

.

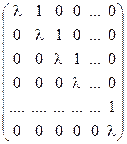Порядок жордановой клетки может быть любым. В частности, если k = 1, то клетка имеет простейший вид : (λ)

Def: Жордановой матрицей называется матрица вида: 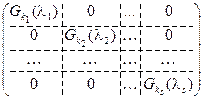. Здесь G_k(λ) – жордановы клетки.

В частности, если оператор А имеет матрицу 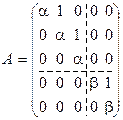, то нормальная жорданова форма матрицы оператора состоит из двух жордановых клеток. Нетрудно заметить, что a и β – соответственные значения оператора А. И, кроме того:

Ае₁ = aе₁; Ае₂ = aе₂ + е₁; Ае₃ = aе₃ + е₂; Ае₄ = bе₄; Ае₅ = bе₅ + е₄.

Тº. Произвольный линейный оператор А в комплексном пространстве V имеет базис

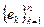, в котором матрица оператора А имеет жорданову форму.

Доказательство теоремы довольно громоздко и мы его не приводим. Построение базиса и приведение матрицы оператора к жордановой форме продемонстрируем на примерах.