Схема нахождения нормальной жордановой формы матрицы оператора и построения жорданова базиса.

Схема построена на построении циклических инвариантных подпространств, которые были рассмотрены в первой части нашего курса.

1. Нахождение собственных векторов и собственных значений оператора А. Если количество собственных линейно независимых векторов равно размерности пространства, то в указанном базисе матрица оператора имеет диагональный вид;

2. Если для кратного собственного значения кратности k количество линейно независимых собственных векторов также равно k, то в этом базисе матрица также имеет диагональный вид;

3. Для кратных собственных значений l таких, что количество линейно независимых собственных векторов меньше кратности корня, поиск базисных векторов производится так:

а) находим собственные векторы А, т.е. базис N(A_l) ядра оператора А_l = А – lЕ;

б) находим М(А_l) – образ оператора А_l и его базис;

в) ищем базис М(А_l) ∩ N(А_l) ;

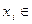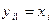г) для каждого вектора М(А_l) ∩ N(А_l) находим прообраз 1-го слоя такой, что: А_l , прообраз 2-го слоя такой, что: А_l 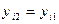, и т.д. до тех пор пока они есть.

Жорданов базис формируется следующим образом:

а) первыми в базис попадают базисные векторы ядра оператора А_l вместе со своими прообразами: х₁, y₁₁, y₁₂, …, х₂, y₂₁, y₂₂,… …, х_р, y_p1, y_p2….

б) затем в базис включаются векторы х_p+1, х_p+2, …, х_l, дополняющие базис М(А_l) ∩ N(А_l) до базиса ядра оператора А_l , если такие есть.

* Замечание: Процесс проводится для каждого значения l до тех пор пока количество векторов, включенных в базис не станет равным кратности k собственного значения l.

Искомый базис: х₁, y₁₁, y₁₂, …, х₂, y₂₁, y₂₂,… …, х_р, y_p1, y_p2…., х_p+1, х_p+2, …, х_l.

(Всего k векторов).